Caiu no vestibular

O encontro das águas

(International Junior Science Olympiad - IJSO)
No estado do Amazonas ocorre o encontro das águas entre o rio Negro, de água negra, e o rio Solimões, de água barrenta. As águas dos dois rios correm lado a lado sem se misturar ao longo de 10 km. Três fatores principais explicam a ocorrência deste fenômeno: as diferenças entre as densidades das águas, de suas temperaturas e das velocidades de suas correntezas: a velocidade da correnteza do rio Negro é de aproximadamente 2 km/h, a uma temperatura de 28°C, enquanto que a velocidade da correnteza do rio Solimões varia de 4 km/h a 6 km/h, sendo sua temperatura de 22°C.
O Instituto do Patrimônio Histórico e Artístico do Brasil (Iphan) declarou o encontro dos rios como patrimônio cultural.

Com base no texto acima responda as questões 1 e 2:

1. A diferença entre as temperaturas dos rios Negro e Solimões é igual a:
a) 279 K
b) 42,8 ºF
c) 298 K
d) 10,8 ºF
e) 28K

Resolução:

Δθ_C = (28 - 22) ºC = 6,0 ºC
ΔT = Δθ_C => ΔT = 6,0 K
Δθ_C/5 = Δθ_F/9 => 6,0/5 = Δθ_F/9 => Δθ_F = 10,8 ºF
 

Resposta: d

2. Partindo de um ponto situado no rio Negro uma canoa desenvolve em relação às águas a velocidade de 10 km/h numa direção perpendicular à linha divisória entre os rios, atingindo um ponto do rio Solimões. Considere as velocidades das correntezas, respectivamente, 2 km/h e 6 km/h e os locais de partida e de chegada situados a 2 km em relação à linha divisória dos rios. Nestas condições, a canoa é arrastada, pela correnteza dos rios, uma distância total de:
a) 0,4 km
b) 1,2 km
c) 1,6 km
d) 2,0 km
e) 3,6 km

Resolução:

  
Semelhança de triângulos:
AB/2 km/h = 2 km/10 km/h => AB = 0,4 km
CD/6 km/h = 2 km/10 km/h => CD = 1,2 km
Distância total rio abaixo: 0,4 km + 1,2 km = 1,6 km

Resposta: c

Cursos do Blog - Eletricidade

Lei de Pouillet. Associação de geradores.
x
Borges e Nicolau
x
Considere o circuito constituído de um gerador ligado aos terminais de um resistor. Este circuito é percorrido por uma corrente somente e é denominado circuito simples.

A tensão elétrica entre os polos do  gerador (U = E – r.i) é igual à tensão elétrica no resistor (U = R.i). Portanto, podemos escrever:

E - r.i = R.i

E = (r + R).i

i = E/(r + R)

Esta fórmula que permite calcular a intensidade da corrente elétrica num circuito simples recebe o nome de Lei de Pouillet, em homenagem ao físico francês Claude Pouillet.
Se o gerador estiver ligado a uma associação de resistores, determina-se a resistência equivalente R_eq e, a seguir, aplica-se a Lei de Pouillet:

i = E/(r+R_eq)

x
Se tivermos uma associação de geradores, determinamos a fem equivalente e, a seguir, aplicamos a lei de Pouillet. Exemplos:

1º)

i = 3E/(3r+R)

2º)
x

 i = E/[(r/3)+R]

x
Exercícios básicos

Exercício 1:
Considere o circuito abaixo. Determine as leituras do amperímetro e do voltímetro, considerados ideais.

Resolução:

Lei de Pouillet:
i = E/(r+R) => i = 6/(1+2) => i = 2 A (leitura do amperímetro)
Leitura do Voltímetro:
U = E – r.i => U = 6 – 1.2 => U = 4 V

Respostas: 2 A; 4 V

Exercício 2:
Determine a intensidade da corrente que atravessa o circuito simples esquematizado abaixo. Ao lado do circuito são representadas as curvas características do gerador e do resistor.

Resolução:

Da curva característica do gerador, tiramos: E = 12 V e I_CC = 6 A.
Sendo I_CC = E/r vem: 6 = 12/r => r = 2 Ω
Da curva característica do resistor: U = R.i => 6 = R.2 => R = 3 Ω
Lei de Pouillet:
i = E/(r+R) => i = 12/(2+3) => i = 2,4 A

Resposta: 2,4 A

Exercício 3:
Para o circuito esquematizado, determine as intensidades das correntes i, i₁ e i₂.

Resolução:

Inicialmente devemos calcular a R_eq: os resistores de 2 Ω e 4 Ω estão ligados em série, sendo 6 Ω a resistência desta associação. Os resistores de 6 Ω e 3 Ω estão em paralelo. A resistência equivalente da associação toda é R_eq = 2 Ω
Lei de Pouillet:
i = E/(r+R_eq) => i = 12/(2+2) => i = 3 A
A ddp no resistor equivalente de 2 Ω é a mesma ddp nos resistores de 3 Ω e de 6 Ω (2 Ω + 4 Ω): U = 2.3 => U = 6 V.
Cálculo de i₁: U = R₁.i₁ => 6 = 6.i₁ => i₁ = 1 A
Cálculo de i₂: U = R₂.i₂ => 6 = 3.i₂ => i₂ = 2 A

Respostas: 3 A; 1 A; 2 A

Exercício 4: 
Determine a leitura do amperímetro ideal inserido no circuito, conforme indicado a seguir. 

Resolução:

i = 3E/(3r+R) => i = 18/(3+9) => i = 1,5 A

Resposta: 1,5 A

Exercício 5: 
Determine a leitura do amperímetro ideal inserido no circuito abaixo.

  
Resolução:

i = E/[(r/3)+R] => i = 6/[(1/3)+3] => i = 1,8 A

Resposta: 1,8 A

Cursos do Blog - Termologia, Óptica e Ondas

Imagem de um objeto extenso. Associação de espelhos planos.

Borges e Nicolau

Imagem de um objeto extenso

Considere um objeto extenso colocado em frente de um espelho plano. Para obtermos a imagem deste objeto basta aplicar a propriedade de simetria para cada um de seus pontos.

Observe que a imagem tem as mesmas dimensões do objeto e é direita em relação ao objeto.

O espelho plano não inverte a imagem mas troca o lado direito do objeto pelo lado esquerdo e vice-versa.

Associação de espelhos planos

Considere dois espelhos planos dispostos de modo que suas superfícies refletoras formem um certo ângulo α. Quando 360º/α for inteiro, o número N de imagens é dado por:

N = (360º/α) - 1

Se 360º/α for par a fórmula anterior vale qualquer que seja a posição do objeto.
Se 360º/α for ímpar a fórmula vale para o objeto no plano bissetor de α.

Foto 1

Na foto 1 temos α = 90º e observamos 3 imagens.
Conferindo N = (360º/90º) - 1 => N = 4 - 1 => N = 3 imagens

Foto 2

Na foto 2, α = 60º e observamos 5 imagens.
Conferindo N = (360º/60º) - 1 => N = 6 - 1 => N = 5 imagens

Exercícios básicos

Exercício 1:
Obtenha a imagem do objeto ABCD formada pelo espelho plano E.

Resolução:

Para obtermos a imagem deste objeto basta aplicar a propriedade de simetria para cada um de seus pontos.

Exercício 2:
Uma pessoa de altura H está diante de um espelho plano vertical. A representa a cabeça, B seus pés e O os seus olhos.
a) Trace os raios de luz que partem de A e B, sofrem reflexão no espelho e chegam aos olhos O da pessoa.
b) Prove que o tamanho mínimo do espelho para que a pessoa possa se ver de corpo inteiro não depende de sua distância ao espelho e é igual a H/2.

Resolução:

a) Achamos A’, imagem de A. Unimos A’ ao olho O. Encontramos o ponto F. Traçamos o raio incidente AF e o raio refletido FO. O mesmo raciocínio fazemos para o ponto B.

b) Da semelhança dos triângulos A'B'O e FGO vem:
H/e = 2d/d => e = H/2
Portanto, o tamanho mínimo do espelho para que a pessoa possa se ver de corpo inteiro não depende de sua distância ao espelho (note que a distância d é cancelada) e é igual à metade da altura da pessoa.

Exercício 3:
Olhando pelo espelho retrovisor plano de seu automóvel um motorista lê, no pára-choque do caminhão que está atrás, a frase NÃO CORRA. Como esta frase foi escrita no para-choque?

Resolução:

O espelho plano não inverte a imagem, mas troca a direita pela esquerda e vice-versa. Assim, temos:

Exercício 4:
Dois espelhos planos formam entre si um ângulo de 30º. Um pequeno objeto é colocado entre os espelhos. O número de imagens que se forma é igual a:
a) 9  b) 10  c) 11  d) 12  e) 13

Resolução:

N = (360º/α) - 1 => N = (360º/30º) - 1 => N = 11 imagens

Resposta: c

Exercício 5:
Um fotógrafo coloca três velas entre dois espelhos planos e consegue obter uma foto onde aparecem no máximo 24 velas. Um valor possível do ângulo entre os espelhos é de:
a) 90º  b) 60º  c) 45º  d) 30º  e) 20º

Resolução:

Aparecendo na foto 24 velas, concluímos que as três velas formam 21 imagens. Assim, para cada vela temos 7 imagens. Portanto:
N = (360º/α) - 1 => 7 = (360º/α) - 1 => 8 = (360º/α) => α = 45º

Resposta: c

Cursos do Blog - Mecânica

Aplicando as Leis de Newton (II)

Borges e Nicolau

Leis de Newton

Primeira lei

Um ponto material isolado ou está em repouso ou realiza movimento retilíneo uniforme.

Segunda lei

A resultante das forças aplicadas a um ponto material é igual ao produto de sua massa pela aceleração adquirida:

F_R = m.a

Terceira lei

Quando um corpo 1 exerce uma força F12 sobre um corpo 2, este exerce no primeiro outra força F21 de mesma intensidade, mesma direção e sentido oposto.

Exercícios básicos

Exercício 1:
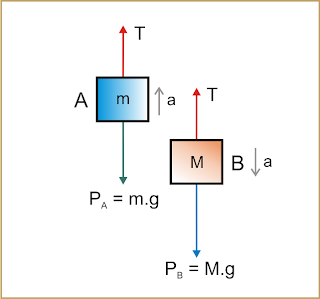
O dispositivo representado na figura, conhecido como máquina de Atwood, é constituído por dois blocos, A e B, de massas m e M, ligados por um fio ideal que passa por uma polia também ideal.

Considere  M = 3,0 kg, m = 2,0 kg e g = 10 m/s².

a) Represente as forças que agem em A e B
b) Aplique a segunda lei de Newton aos blocos e calcule a intensidade da aceleração de A e B e a intensidade da força de tração no fio que envolve a polia
c) A intensidade da força de tração no fio OC

Resolução:

a)

b)
PFD (A): T - m.g = m.a => T – 20 = 2.a (1)
PFD (B): M.g - T = M.a => 30 – T = 3.a (2)
(1) + (2): 30 – 20 = (2 + 3).a => a = 2,0 m/s²
De (1): T - 20 = 2.2,0 => T = 24 N

c) Isolando a polia, temos: T_OC = 2T => T_OC = 48 N

Respostas:
b) 2,0 m/s²; 24 N
c) 48 N

Exercício 2:
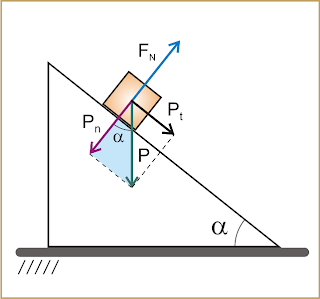
Uma caixa escorrega num plano inclinado perfeitamente liso. Seja α o ângulo que o plano inclinado forma com a horizontal (figura a). Na caixa agem as forças: seu peso de intensidade P e a força normal de intensidade F_N (figura b). Na figura c a força peso foi decomposta nas componentes P_n perpendicular ao plano inclinado e P_t tangente ao plano.

 Clique para ampliar

Prove que:

a) P_n = P.cosα e P_t = P.senα
b) A caixa escorrega com aceleração de intensidade a = g.senα

Resolução:

a)
senα = P_t/P => P_t = P.senα
cosα = P_n/P => P_n = P.cosα

b)
Segunda lei de Newton
P_t = m.a
m.g.senα = m.a
a = g.senα

Exercício 3:
Considere dois blocos A e B de massas m = 2.0 kg e M = 3,0 kg, respectivamente. O bloco A está apoiado numa plano inclinado perfeitamente liso e é ligado, por um fio ideal, ao bloco B que se move verticalmente. Considere g = 10 m/s². Determine a intensidade da aceleração dos blocos e a intensidade da força de tração no fio.

Resolução:

PFD (A): T - 10 = 2,0.a  (1)
PFD (B): 30 – T = 3,0.a (2)
(1) + (2): 30 - 10 = (2,0 + 3,0).a => a = 4,0 m/s²
De (1): T – 10 = 2,0.4,0 => T = 18 N
 
Respostas: 4,0 m/s²; 18 N

Exercício 4:
Uma esfera de massa m = 1,0 kg é suspensa por um fio ideal ao teto de um elevador, conforme mostra a figura a. Na figura b representamos as forças que agem na esfera: seu peso de intensidade P e a força de tração de intensidade T.

Sendo g = 10 m/s², determine T nos casos:

a) O elevador está parado.
b) O elevador sobe em movimento uniforme.
c) O elevador sobe acelerado com aceleração a = 2,0 m/s²
d) O elevador desce acelerado com aceleração a = 2,0 m/s²
e) O elevador desce em queda livre (a = g).

Resolução:

a) O elevador está parado: T = P => T = 10 N

b) O elevador sobe em movimento uniforme: T = P => T = 10 N

c) O elevador sobe acelerado com aceleração a = 2,0 m/s²
T – P = m.a => T – 10 = 1,0.2,0 => T = 12 N

d) O elevador desce acelerado com aceleração a = 2,0 m/s²
P – T = m.a => 10 – T = 1,0.2,0 => T = 8,0 N

e) O elevador desce em queda livre (a = g).
P – T = m.g => P - T = P => T = 0

Respostas: a) 10 N; b) 10 N; c) 12 N; d) 8,0 N; e) zero

Exercício 5:
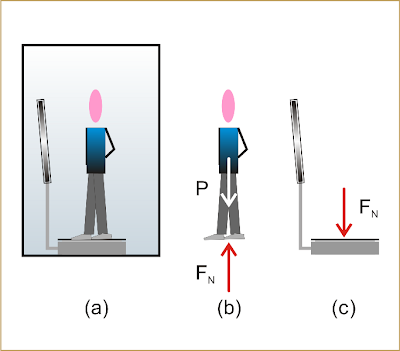
No interior de um elevador coloca-se uma balança graduada em newtons. Uma pessoa de massa 60 kg está sobre a balança (figura a). As forças que agem na pessoa são: seu peso de intensidade P e a força normal de intensidade FN (figura b). A reação da força normal que age na pessoa está aplicada na balança (figura c).
A balança marca F_N.

Sendo g = 10 m/s², determine a indicação da balança  nos casos:

a) O elevador está parado.
b) O elevador sobe em movimento uniforme.
c) O elevador sobe acelerado com aceleração a = 2,0 m/s²
d) O elevador desce acelerado com aceleração a = 2,0 m/s²
e) O elevador desce em queda livre (a = g).

Resolução:

a) O elevador está parado: F_N = P = 600 N

b) O elevador sobe em movimento uniforme: F_N = P = 600 N

c) O elevador sobe acelerado com aceleração a = 2,0 m/s²
F_N - P = m.a => F_N - 600 = 60.2,0 => F_N = 720 N

d) O elevador desce acelerado com aceleração a = 2,0 m/s²
P -  F_N = m.a => 600 - F_N = 60.2,0 => F_N = 480 N

e) O elevador desce em queda livre (a = g).
P - F_N = m.g  => P - F_N = P => F_N = 0 (A pessoa não comprime a balança, flutuando dentro do elevador)

Respostas: a) 600 N; b) 600 N; c) 720 N; d) 480 N; e) zero

Arte do Blog

 

La promesse

René Magritte

René Magritte nasceu em Lessines, na província de Hainaut, em 1898. Pouco se sabe sobre a sua vida além do fato de ter começado a ter aulas de desenho em 1910. Um fato marcante, em 12 de março de 1912, sua mãe cometeu suicídio afogando-se no Rio Sambre. Há uma lenda que diz que Magritte, com 13 anos, presenciou a retirada do corpo da água e ficou impressionado com o vestido cobrindo o rosto de sua mãe. Essa imagem é apontada como inspiração para vários quadros pintados nos anos da década de 1920 nos quais há pessoas com panos encobrindo os rostos, incluindo Les Amants.

La Trahison des Images

As primeiras pinturas de Magritte são de 1915, com influência do impressionismo. Entre 1916 e 1918 ele estudou na Academie Royale des Beaux-Arts, em Bruxelas, sob a batuta de Montald Constant, mas não encontrou inspiração para criar um estilo próprio. As pinturas produzidas entre 1918 e 1924 tiveram inspiração no futurismo e no cubismo praticado por Metzinger. A maioria das obras desse período são nus femininos.

Time Transfixed

Em 1922 Magritte se casou com Georgette Magritte Berger, que conhecia desde 1913 quando ainda era uma criança. Em 1926 um contrato com a Galerie la Centaure em Bruxelas tornou possível a ele pintar em tempo integral e é dessa época a sua primeira pintura a óleo surreal, O Jockey Lost (Le jockey perdu). A primeira exposição de Magritte aconteceu em Bruxelas, em 1927. Foi um fiasco total, a crítica o detonou. Deprimido ele se mudou para Paris, onde se tornou amigo de André Breton, e envolveu-se no grupo surrealista.

 

Not to be Reproduced

Durante a ocupação alemã da Bélgica, na Segunda Guerra Mundial, Magritte permaneceu em Bruxelas, o que levou a uma ruptura com Breton. Por um breve período ele adotou um estilo colorido nos anos de 1943 e 1944, seu "Período de Renoir". Fica claro que tratou-se de uma reação aos sentimentos de alienação e abandono resultantes da Bélgica ocupada. Nos anos difíceis de 1947 e 1948, Magritte pintou Picassos, Braques e Chiricos, um repertório de quadros falsos para prover o básico no período de escassez do pós-guerra. Este empreendimento foi realizado em sociedade com seu irmão Paulo Magritte e Marcel Marien, a quem coube a tarefa de vender as falsificações. No final de 1948, ele voltou para o estilo e os temas de sua arte surrealista pré-guerra.

Le Jockey Perdu

Seus trabalhos foram exibidos pela primeira vez nos Estado Unidos em 1936, em Nova York e, novamente, naquela cidade, em duas exposições retrospectivas, uma no Museu de Arte Moderna, em 1965, e outra no Metropolitan Museum of Art, em 1992. Magritte morreu de câncer no pâncreas em 15 de agosto de 1967, em sua própria cama, e foi enterrado no Cemitério de Schaerbeek, Evere, Bruxelas. O interesse popular na obra de Magritte aumentou consideravelmente na década de 1960, e sua imaginação influenciou a arte pop, minimalista e conceitual.

 

Les Amants

Saiba mais aqui e aqui    

Colaboradores do Blog

Hoje tem início uma nova seção do Blog

Borges e Nicolau

Conforme havíamos combinado, inauguramos hoje o espaço dos colaboradores do Blog. Para tanto estamos publicando um vídeo criado a partir de uma apresentação em PowerPoint de autoria do professor Willian Rederde.

Participe você também, seus alunos ficarão orgulhosos.

Especial de Sábado

Ganhadores do Premio Nobel de Física

Borges e Nicolau

x

1967
Hans Albrecht Bethe pelas suas contribuições à teoria das reações nucleares.

Hans Albrecht Bethe (1906-2005), físico alemão

Hans Albrecht Bethe estudou Física em Frankfurt e fez seu doutoramento na Universidade de Munique. Quando os nazistas chegaram ao poder deixou a Alemanha, emigrando para a Inglaterra e depois para os Estados Unidos onde foi professor na Universidade de Cornell. Em 1967 recebeu o premio Nobel de Física pelas suas contribuições à teoria das reações nucleares, especialmente por suas descobertas relativas à produção de energia nas estrelas. Foi um grande defensor do uso pacífico da energia nuclear.

Saiba mais. Clique aqui

Próximo Sábado: Ganhador do Premio Nobel de 1968:

Luis Walter Alvarez por suas contribuições ao estudo da Física das partículas elementares.

A Física Explica

Plasma: dos antigo gregos à televisão que você quer ver 

Professor Felipe Damasio 
Colégio São Bento, Criciúma, SC 
Professor Gilberto Calloni 
Colégio São José, Caxias do Sul, RS 
Fonte: A Física na Escola 

Clique aqui

Caiu no vestibular

Deformando a mola

(FGV – Economia)
Em algumas estações de trem há rígidas molas no fim dos trilhos com a finalidade de amortecer eventual colisão de um trem, cujo maquinista não consiga pará-lo corretamente junto à plataforma. Certa composição, de massa total 2m, parada bem próximo à mola de constante k, relaxada, recebe um impacto de outra composição, de massa m, vindo a uma velocidade v, que acaba engatando na primeira. Ambas vão comprimir a mola, causando-lhe uma deformação máxima x ao pararem instantaneamente, como mostram os esquemas.

Desprezando a ação de agentes externos e dissipativos, a expressão de x, em função de k, m e v, será

a) x = (m.v) / (3.k).

b) x = (m.v²) / (3.k).
c) x = (v/3).√(m/k).
d) x = v.√(3.m)/k.
e) x = v.√(m/(3k).

Resolução:

Conservação da quantidade de movimento:
Sendo v a velocidade da composição de massa m e v’ a velocidade das composições engatadas, temos:

Q_antes = Q_depois => m.v = 3m.v' => v' = v/3

Conservação da Energia Mecânica:

k.x²/2 = 3m.(v/3)²/2 => x = v.√(m/(3k)

Resposta: e