Caiu no vestibular

Circuito com chave

(UNESP–SP)
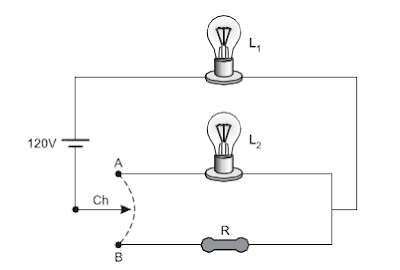
Considere o circuito elétrico que esquematiza dois modos de ligação de duas lâmpadas elétricas iguais, com valores nominais de tensão e potência elétrica 60 V e 60 W, respectivamente.

Modo A – ambiente totalmente iluminado: a chave Ch, ligada no ponto A, mantém as lâmpadas L1 e L2 acesas.
Modo B – ambiente levemente iluminado: a chave Ch, ligada no ponto B, mantém apenas a lâmpada L1 acesa, com potência menor do que a nominal, devido ao resistor R de resistência ôhmica constante estar ligado em série com L1.

Considerando que as lâmpadas tenham resistência elétrica constante, que os fios tenham resistência elétrica desprezível e que a diferença de potencial de 120 V que alimenta o circuito seja constante, calcule a energia elétrica consumida, em kWh, quando as lâmpadas permanecem acesas por 4 h, ligadas no modo A – ambiente totalmente iluminado.

Determine a resistência elétrica do resistor R, para que, quando ligada no modo B, a lâmpada L1 dissipe uma potência de 15 W.

Resolução:

Ligação segundo o modo A

Neste caso, as lâmpadas L1 e L2 estão em série e a associação está sob ddp total de 120 V. Cada lâmpada fica sob ddp de 60 V e, portanto, ambas estão funcionado normalmente.
A energia elétrica consumida pelas lâmpadas em 4 h será:

Eel = PTotal.Δt => Eel = [(60+60)/1000] kW.4h => Eel = 0,48 kWh

Ligação segundo o modo B

Vamos calcular a resistência elétrica RL de cada lâmpada pelos dados nominais.

P = U²/RL => 60 = 60²/RL => RL = 60 Ω.

Conforme o enunciado a resistência elétrica de cada lâmpada é constante. Cálculo da intensidade da corrente que percorre a lâmpada L1 e o resistor de resistência R:

P = RL.i² => 15 = 60.i² => i = 0,50 A
De UTotal = (R+RL).i, vem: 120 = (R+60).0,50 => R = 180 Ω

Respostas: 0,48 kWh e 180 Ω