Termodinâmica (II)
Borges e Nicolau
Vamos revisar a aula passada e relembrar que no diagrama p x V a área é numericamente igual ao trabalho trocado pelo gás.
A área A é numericamente igual ao trabalho τ na transformação A => B
Recordemos ainda que:
xxxxxxxxxxxxxxV aumenta = > τ > 0: o gás realiza trabalho
xxxxxxxxxxxxxxV diminui = > τ < 0: o gás recebe trabalho
xxxxxxxxxxxxxxV constante: τ = 0
Nesta semana vamos fazer algumas considerações sobre energia interna e enunciar a primeira lei da Termodinâmica.
Energia Interna U de um sistema
É a soma das várias formas de energia das moléculas que constituem o sistema. Na energia interna incluem-se, por exemplo, a energia cinética de translação e rotação das moléculas, a energia cinética devida ao movimento dos átomos que formam as moléculas, a energia potencial de ligação das moléculas.
Para um gás perfeito monoatômico a energia interna U é a energia cinética de translação de suas moléculas:
xxxxxxxxxxxxxxU = Ec
xxxxxxxxxxxxxxU = (3/2).n.R.Tc
xxxxxxxxxxxxxxΔU = (3/2).n.R.ΔT
xxxxxxxxxxxxxx
Para um determinado número de mols de um gás perfeito, quando a temperatura aumenta a energia interna aumenta e a variação de energia interna é positiva. Quando a temperatura diminui a energia interna diminui e a variação de energia interna é negativa. Numa transformação isotérmica, a temperatura é constante, a energia interna é constante e a variação de energia interna é nula.
Resumindo:
xxxxxxxxxxxxxxT aumenta, U aumenta, ΔU > 0
xxxxxxxxxxxxxxT diminui, U diminui, ΔU < 0
xxxxxxxxxxxxxxT constante, U constante, ΔU = 0c
xxxxxxxxxxxxxxNum ciclo:c
xxxxxxxxxxxxxxTinicial = Tfinal, Uinicial = Ufinal, ΔU = 0
Observação: se o gás não for monoatômico, outras formas de energia devem ser levadas em conta como, por exemplo, a energia cinética de rotação das moléculas.
Nestas condições, teremos U > (3/2).n.R.T
Primeira Lei da Termodinâmica
É o princípio da conservação da energia aplicado à Termodinâmica.
Imagine que um gás receba uma quantidade de calor igual Q = 200 J. Vamos supor que o gás se expanda e realize um trabalho τ = 120 J.
Os 80 J restantes ficam armazenados no gás, aumentando sua energia interna (ΔUx=x80 J). As três formas de energia, Q, τ e ΔU relacionam-se, constituindo a primeira lei da Termodinâmica:
xxxxxxxxxxxxxxQ = τ + ΔU
Nos dois resumos anteriores analisamos os sinais de τ e ΔU. Para a quantidade de calor Q, temos:
xxxxxxxxxxxxxxQ > 0: quantidade de calor recebida pelo gás
xxxxxxxxxxxxxxQ < 0: quantidade de calor cedida pelo gás
xxxxxxxxxxxxxxQ = 0: o gás não troca calor com o meio exterior xxxxxxxxxxxxxx(transformação adiabática).
Animação:
Termodinâmica - Noções básicas
Clique aqui
Exercícios básicos
Exercício 1:
Numa transformação isocórica, uma determinada massa de gás recebe a quantidade de calor igual a 1000 J.
a) Determine o trabalho que o gás troca com o meio exterior e a correspondente variação de energia interna.
b) Como se modificariam as respostas anteriores se o gás cedesse uma quantidade de calor de módulo 1000 J?
Resolução: clique aqui
a)
O gás recebe calor => Q = +1000 J
Q = τ + ΔU => V constante: τ = 0 => 1000 = 0 + ΔU => ΔU = +1000 J
b)
O gás cede calor => Q = -1000 J
Q = τ + ΔU => V constante: τ = 0 => -1000 = 0 + ΔU => ΔU = -1000 J
Respostas:
a) τ = 0; ΔU = +1000 J
b) τ = 0; ΔU = -1000 J
Exercício 2:
Numa transformação isotérmica, uma determinada massa de gás recebe a quantidade de calor igual a 1000 J.
a) Determine o trabalho que o gás troca com o meio exterior e a correspondente variação de energia interna.
b) Como se modificariam as respostas anteriores se o gás cedesse uma quantidade de calor de módulo 1000 J?
Resolução: clique aqui
a)
O gás recebe calor => Q = + 1000 J
Q = τ + ΔU => T constante: ΔU = 0 => 1000 = τ + 0 => τ = +1000 J
b)
O gás cede calor => Q = -1000 J
Q = τ + ΔU => V constante: τ = 0 => -1000 = τ + 0 => τ = -1000 J
Respostas:
a) τ = +1000 J; ΔU = 0
b) τ = -1000 J; ΔU = 0
x
Exercício 3:Numa transformação isobárica, 2 mols de um gás perfeito monoatômico recebem uma certa quantidade de calor e consequentemente sua temperatura varia de 300 K a 400 K. Determine:
x
a) o trabalho que o gás troca com o meio exterior;
b) a correspondente variação de energia interna;
c) a quantidade de calor recebida
Dado: R = 8,31 J/mol.K
Resolução: clique aqui
Transformação isobárica:
τ = p.ΔV = n.R.ΔT => τ = 2.8,31.100 => τ = +1662 J
ΔU = (3/2).n.R.ΔT => ΔU = (3/2).2.8,31.100 => ΔU = +2493 J
Q = τ + ΔU => Q = (1662+2493) J => Q = +4155 J
Respostas:
a) τ = +1662 J
b) ΔU = +2493 J
c) Q = +4155 J
Exercício 4:
Numa transformação adiabática, uma determinada massa de gás realiza sobre o meio exterior um trabalho de 1000 J.
a) Determine a quantidade de calor que o gás troca com o meio exterior e a correspondente variação de energia interna.
b) Como se modificariam as respostas anteriores se o gás recebesse do meio exterior um trabalho de módulo 1000 J?
Resolução: clique aqui
Transformação adiabática:
x
Q = 0 => 0 = τ + ΔU => ΔU = -τ
a)
O gás realiza trabalho => τ > 0 => τ = +1000 J => ΔU = -1000 J
b)
O gás recebe trabalho => τ < 0 => τ = -1000 J => ΔU = +1000 J
Respostas:
a) Q = 0; ΔU = -1000 J
b) Q = 0; ΔU = +1000 J
Exercício 5:
Um gás sofre uma compressão ou uma expansão muito rápida. Sendo o intervalo de tempo no qual ocorre a transformação muito pequeno não há tempo para o gás trocar calor com o meio exterior. Nestas condições, a transformação é considerada adiabática.
a) Analise o que ocorre, numa compressão adiabática, com a temperatura T, a energia interna U e a pressão p, dizendo se estas grandezas aumentam ou diminuem? Cite exemplos do dia a dia onde ocorre tal transformação.
b) Analise o que ocorre, numa expansão adiabática, com a temperatura T, a energia interna U e a pressão p, dizendo se estas grandezas aumentam ou diminuem? Cite exemplos do dia a dia onde ocorre tal transformação.
Resolução: clique aqui
a)
Compressão adiabática: T, U e p aumentam
• Ao comprimir rapidamente o ar de uma bomba, ao encher um pneu ou uma bola, nota-se que a bomba se aquece.
• Com a mesma bomba, tampe com um dedo a saída de ar. Comprima rapidamente. Você sentirá um aumento de temperatura.
b)
Expansão adiabática: T, U e p diminuem
• Sopre com a boca aberta sobre sua mão. Você sentirá que o ar sai quente. Sopre agora rapidamente com a boca fazendo um “biquinho”. Você notará que o ar sai bem mais frio.
• Ao acionar um "spray" há uma expansão rápida e o tubo fica mais frio.
Exercícios de revisão
Revisão/Ex 1:
(UF Santa Maria-RS)
Um gás ideal sofre uma transformação: absorve 50 cal de energia na forma de calor e expande-se realizando um trabalho de 300 J. Considerando 1 cal = 4,2 J, a variação da energia interna do gás é, em J, de:
a) 250 b) –250 c) 510 d) –90 e) 90
Resolução: clique aqui
Pela Primeira Lei da Termodinâmica, temos:
Q = τ + ΔU => 50.4,2 J = 300 J + ΔU => ΔU = -90 J: o gás recebeu 210 J de calor, realizou um trabalho de 300 J e a energia interna diminuiu de 90 J.
Resposta: d
Revisão/Ex 2:
(UFLA-MG)
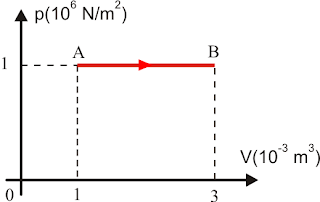
O diagrama pV da figura mostra uma transformação sofrida por 0,4 mol de um gás monoatômico ideal.
Considerando TA = 300 K e TB = 900 K, a quantidade de calor envolvida na transformação será (considere 1 cal = 4 J e R = 2 cal/mol.K):
a) 220 cal b) -1.220 cal c) 2.500 cal d) -2.500 cal e) 1.220 cal
Resolução: clique aqui
A área no diagrama pxV fornece o trabalho. No caso o gás realiza trabalho pois o volume aumenta:
τ = área => τ = (3-1).10-3.1.106 => τ = 2.103 J
A variação de energia interna é dada por:
ΔU = 3/2.n.R.ΔT => ΔU = 3/2.0,4mol.8(J/mol.K).600K => ΔU = 2880 J
Pela Primeira Lei da Termodinâmica, temos:
Q = τ + ΔU => Q = 2000J+2880J => Q = 4880 J = (4880/4)cal = 1220 cal
Resposta: e
Revisão/Ex 3:
(UFRGS)
É correto afirmar que, durante a expansão isotérmica de uma amostra de gás ideal:
a) a energia cinética média das moléculas do gás aumenta.
b) o calor absorvido pelo gás é nulo.
c) o trabalho realizado pelo gás é nulo.
d) o trabalho realizado pelo gás é igual à variação da sua energia interna.
e) o trabalho realizado pelo gás é igual ao calor absorvido pelo mesmo.
Resolução: clique aqui
Na expansão o gás realiza trabalho. Sendo isotérmica, não há variação de energia interna. Logo, o trabalho que o gás realiza é devido ao fato de receber calor. Portanto, o trabalho realizado pelo gás é igual ao calor absorvido pelo mesmo.
Resposta: e
Revisão/Ex 4:
(U.F.Uberlândia-MG)
Um gás ideal é comprimido tão rapidamente que o calor trocado com o meio é desprezível. É correto afirmar que:
a) a temperatura do gás diminui
b) o gás realiza trabalho para o meio exterior
c) a energia interna do gás aumenta
d) o volume do gás aumenta
e) a pressão do gás diminui
Resolução: clique aqui
Na compressão adiabática o gás recebe trabalho do meio exterior. Assim, o volume diminui. Como não há troca de calor, o trabalho recebido se converte em energia interna. Logo, a energia interna aumenta e, portanto, a temperatura aumenta. Como T aumenta e V diminui, concluímos da Equação de Clapeyron que a pressão p aumenta.
Resposta: c
Revisão/Ex 5:
(URCA)
Quando um sistema termodinâmico vai de um estado A para um estado B sua energia interna aumenta de 200 J. Ao retornar ao estado A o sistema cede 80 J de calor à sua vizinhança e realiza trabalho τ. O valor de τ é:
a) 120 J;
b) -120 J;
c) 120 cal;
d) 80 J;
e) 200 J.
Resolução: clique aqui
Se na transformação AB a energia interna aumenta de 200 J, na transformação BA ela diminui de 200 J, ou seja: ΔU = -200 J
Como o gás cede 80 J, temos Q = -80 J.
Pela Primeira Lei da Termodinâmica, temos:
Q = τ + ΔU => -80 = τ + (-200J) => τ = 120 J
Resposta: a

Nenhum comentário:
Postar um comentário