Cursos do Blog - Mecânica

4ª aula
Movimento Uniforme (II)

Borges e Nicolau

Quando resolvemos exercícios de Cinemática precisamos, muitas vezes, escrever as funções horárias dos móveis estudados. Algumas grandezas envolvidas são arbitrárias e dependem de nossa escolha.

Origem dos espaços

Ponto da trajetória a partir do qual medimos os comprimentos que indicam as posições dos móveis. Sua escolha é livre e uma vez fixada será referência para todos os móveis.

Origem dos tempos (t = 0)

Corresponde ao instante em que o cronômetro é disparado.

Orientação da trajetória

Definida a origem dos espaços deve ser escolhida a orientação da trajetória. Com isso ficam determinados os sinais das velocidades escalares. Os móveis que caminham no sentido da orientação da trajetória têm velocidade escalar positiva e os que caminham no sentido oposto, velocidade escalar negativa.

Funções horárias

Tomadas as providências acima, podemos escrever as funções horárias lembrando que no movimento uniforme são do tipo s = s₀ + v.t, onde:

s₀ = Espaço inicial. Espaço do móvel no instante t = 0.

v = velocidade escalar.

Exemplo:

Dois móveis, A e B, distam 400 km. Sabendo-se que partem no mesmo instante e caminham em sentidos opostos, depois de quanto tempo se encontrarão? O móvel A tem velocidade de módulo igual a 60 km/h e o móvel B, 40 km/h. A que distância do ponto de partida do móvel A ocorre o encontro entre os móveis?

Resolução:

Escolhemos a origem dos espaços no ponto de partida do móvel A.

Orientamos a trajetória de A para B. (Escolha arbitrária, poderíamos ter escolhido a origem no ponto de partida de B e orientado a trajetória

de B para A. O resultado seria o mesmo.)

O espaço inicial de A é igual a zero. s_0A = 0.

O espaço inicial de B é igual a 400 km. s_0B = 400 km.

A velocidade escalar de A é positiva. v_A = 60 km/h.

A velocidade escalar de B é negativa. v_B = -40 km/h.

Com esses dados escrevemos as funções horárias dos móveis A e B:

s_A = s_0A + v_At

s_A = 0 + 60t

s_B = s_0B + v_Bt

s_B = 400 – 40t

No instante do encontro os móveis têm espaços iguais.

s_A = s_B

60t = 400 – 40t

100t = 400

t = 4 h

Os móveis encontram-se 4 h após a partida.

Local do encontro:

Substituindo-se t = 4 h na função horária do móvel A, temos:

s_A = 60.4

s_A = 240 km

O encontro se dá a 240 km do ponto de partida do móvel A.

Velocidade escalar relativa

O instante do encontro poderia ser obtido por velocidade escalar relativa. Nesse caso o móvel B seria tomado com referencial e o módulo da velocidade escalar do móvel A, em relação a B, passaria a ser a soma dos módulos das velocidades dos móveis A e B, em relação ao solo.

Assim v_relat = (60 + 40) km/h, v_relat = 100 km/h.

v_relat = distância inicial entre os móveis/intervalo de tempo do encontro (t)

100 = 400/t

t = 4 h

Nota: Quando os móveis deslocam-se em sentidos opostos o módulo da velocidade escalar relativa é a soma dos módulos das velocidades escalares. Quando os móveis deslocam-se no mesmo sentido o módulo da velocidade escalar relativa é a diferença dos módulos das velocidades escalares.

Exercícios básicos

Exercício 1:

Dois automóveis, A e B, percorrem trajetórias retas e paralelas com velocidades de módulos 50 km/h e 80 km/h, em relação ao solo. Qual é o módulo da velocidade escalar do carro B, em relação ao carro A. Analise os casos:

a) A e B deslocam-se no mesmo sentido.

                                  A                                          B

b) A e B deslocam-se em sentidos opostos.

                                 A                                           B

Resolução:

a) v_relat = v_B - v_A = 80 km/h - 50 km/h = 30 km/h

b) v_relat = v_B + v_A = 80 km/h + 50 km/h = 130 km/h

Respostas:

a) 30 km/h

b) 130 km/h

Exercício 2:

Dois trens T₁ e T₂ percorrem trajetórias retas, paralelas e no mesmo sentido. O trem T₁ tem comprimento igual a 300 m e velocidade constante de módulo 90 km/h. O trem T₂ tem comprimento igual a 150 m e velocidade constante de módulo 72 km/h. Determine:

a) O intervalo de tempo necessário para que o trem T₁ ultrapasse o trem T₂.

b) A distância percorrida pelo trem T₁ durante a ultrapassagem.

Resolução:

a) Vamos resolver este item por velocidade relativa. Em relação ao trem T₂ o trem T₁ possui velocidade: v_relat = v₁ - v₂ = 90 km/h - 72 km/h = 18 km/h = 5 m/s.

Cada ponto do trem T₁ percorre, em relação a T₂, a distância de 450 m, durante a ultrapassagem:
x

v_relat = Δs_relat/Δt => 5 = 450/Δt => Δt = 90 s.

b) Em 90 s o trem T₁ percorre a distância: 

Δs₁ = v₁.Δt = (90/3,6).90 => Δs₁ = 2250 m.

Respostas:

a) 90 s

b) 2250 m

Exercício 3:

Resolva o exercício anterior considerando que os trens se desloquem em sentidos contrários.

Resolução:

a) v_relat = v₁ + v₂ = 90 km/h + 72 km/h = 162 km/h = 45 m/s.
v_relat = Δs_relat/Δt => 45 = 450/Δt => Δt = 10 s.

b) Em 10 s o trem T₁ percorre a distância:
Δs₁ = v₁.Δt = (90/3,6).10 => Δs₁ = 250 m. 

Respostas:

a) 10 s

b) 250 m 

Exercício 4:

Dois carros, A e B, partem de São Paulo com destino a Mairiporã, desenvolvendo em todo trajeto movimentos uniformes de mesma velocidade de módulo 60 km/h. O carro A partiu 20 minutos antes do que o carro B. Um carro C parte de Mairiporã com destino a São Paulo, também realizando movimento uniforme. O carro C cruza com o carro A e 12 minutos depois cruza com o carro B. Determine o módulo da velocidade do carro C. 

Resolução:

Quando o carro B parte, o carro A já percorreu 60 (km/h) x 1/3 (h) = 20 km. Como as velocidades de A e B são constantes e iguais esta distância permanece constante. A velocidade relativa do carro C, em relação aos carros A e B é (v_c + 60) km/h. Com essa velocidade o carro C percorre 20 km em 12 min = 1/5 (h).

Assim, temos:

v_c + 60 = 20/(1/5) => v_c + 60 = 100 => v_c = 40 km/h

Resposta: 40 km/h

Exercício 5:

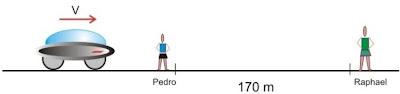
Dois estudantes Pedro e Raphael realizam uma experiência visando determinar, numa rodovia, a velocidade escalar de um carro que realiza um movimento retilíneo e uniforme.

Pedro está provido de um apito e Raphael de um cronômetro. Os estudantes ficam à distância D = 170 m e no instante em que o carro passa por Pedro ele aciona o apito. Ao ouvir o som do apito, Raphael dispara o cronômetro e o trava no instante que o carro passa por ele. O cronômetro registra 6,3 s. Qual é a velocidade do carro? Sabe-se que a velocidade do som é de 340 m/s.

Resolução:

Cálculo do Intervalo de tempo que o som demora para ir da posição onde está Pedro até a posição onde está Raphael:

v_s = D/Δts => 340 = 170/Δt_s => Δt_s = 0,5 s

Cálculo do intervalo de tempo que o carro demora para ir da posição onde está Pedro até a posição onde está Raphael:

Δt = 6,3 s + 0,5 s 

Velocidade do carro:

v = D/Δt = 170 m/6,8 s = 25 m/s

Resposta: 25 m/s 

Exercícios de Revisão 

Revisão/Ex 1: 
(UFGD)
De duas cidades A e B, separadas por 300 km, partem dois carros no mesmo instante e na mesma direção, porém em sentidos opostos, conforme a figura a seguir. Os dois carros estão em movimento retilíneo uniforme. O carro da cidade A parte com velocidade inicial de 20 m/s; o carro da cidade B, 30 m/s. A distância da cidade A, quando os dois carros se cruzam, é? 

(A) 120 km
(B) 150 km
(C) 180 km
(D) 200 km
(E) 100 km 

Resolução:

Adotando-se a origem dos espaços na posição inicial de A e orientando a trajetória de A para B, temos as funções horárias: 
s_A = 0 + 72.t e s_B = 300 – 108.t
No instante em que os carros se cruzam, temos: 
s_A = s_B => 72.t = 300 – 108.t => t = (300/180)h = (5/3)h. s_A = 0 + 72.t => s_A = 72.(5/3) km = 120 km 

Resposta: A 

Revisão/Ex 2: 
(ETEC-SP)
O Sol, responsável por todo e qualquer tipo de vida em nosso planeta, encontra-se, em média, a 150 milhões de quilômetros de distância da Terra. Sendo a velocidade da luz 3.10⁵ km/s pode-se concluir que, a essa distância, o tempo gasto pela irradiação da luz solar, após ser emitida pelo Sol até chegar ao nosso planeta é, em minutos, aproximadamente,
 
(A) 2.
(B) 3.
(C) 5.
(D) 6.
(E) 8.

Resolução:

Sendo a propagação da luz um movimento uniforme, temos:

v = Δs/Δt => 3.10⁵ = 150.10⁶/Δt => Δt = 500 s = 8 min 20 s

Resposta: E

Revisão/Ex 3:
(IJSO)
O intervalo de tempo entre você ouvir o relâmpago e ver o trovão é Δt segundos. Dado que a velocidade do som é de 340 m/s e a velocidade da luz no vácuo é 3.10⁸ m/s, então a distância aproximada em quilômetros entre você e o relâmpago é de:

A.   Δt/2
B.   Δt/3
C.   Δt/4
D.   Δt/5

Resolução:

Como a velocidade de propagação da luz é muito maior do que a do som, podemos considerar que o relâmpago é visto imediatamente após a sua formação e que o som produzido demora um certo intervalo de tempo para chegar ao observador. Por isso, o cálculo da distância  mencionada é feito utilizando a velocidade do som. 

v = Δs/Δt = 0,340 km/h = Δs/Δt => Δs = Δt.0,340 km

Mas sendo 0,340 km aproximadamente (1/3) km, vem: Δs ≅ Δt/3 km

Resposta: B    

Revisão/Ex 4:
(UEMG)
Dois corpos movimentam-se com velocidade constante na mesma direção, mas em sentidos contrários, afastando-se um do outro. O corpo A tem uma velocidade de 4,0 m/s e o B, de 6,0 m/s. Num certo instante a distância entre eles é de 250 m.
Assinale a alternativa que apresenta o valor da distância entre eles imediatamente após 10 s do instante citado.

A)   150 m.
B)   350 m.
C)   250 m.
D)   100 m.

Resolução:

Adotando-se a origem dos espaços na posição inicial de A e orientando a trajetória de A para B, temos as funções horárias:

s_A = 0 – 4,0.t  e s_B = 250 + 6,0.t

Para t = 10 s, temos s_A = -40 m e s_B = 310 m

A distância entre A e B no instante t = 10 s é dada por:

D = s_B - s_A = 310 - (-40) => D = 350 m

Resposta: B

Revisão/Ex 5
(UCG-GO)
A figura abaixo mostra a posição de um móvel, em movimento uniforme, no instante t = 0. Sendo 5,0 m/s o módulo de sua velocidade escalar, pede-se:

a) a função horária dos espaços;
b) o instante em que o móvel passa pela origem dos espaços.

Resolução:

a) De s = s₀ + v.t e sendo s₀ = 30 m e v = -5,0 m/s, vem: s = 30 - 5,0.t  (SI)
b) para s = 0, temos: 0 = 300 - 5,0.t => t = 6,0 s

Respostas: 
a) s = 30 - 5,0.t  (SI)
b) 6,0 s