x
Borges e NicolauTrabalho de uma força constante segundo uma trajetória retilínea
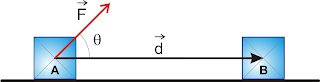
Uma caixa está sendo deslocada numa superfície horizontal, segundo uma trajetória retilínea, passando da posição A para a posição B. Seja d o vetor deslocamento. Das forças que agem na caixa, vamos considerar a força F, constante e que forma um ângulo θ com d.
Por definição, o trabalho τ realizado pela força constante F no deslocamento d é a grandeza escalar:
τ = F.d.cos θ
Quando τ < 0, o trabalho é chamado Resistente
x
Quando τ > 0, o trabalho é chamado Motor
No Sistema Internacional (SI) a unidade de trabalho é o newton x metro que recebe o nome de joule: 1 N.m = 1 J
Casos particulares:
• A força F tem a mesma direção e o mesmo sentido do deslocamento d
(θ = 0º)
τ = +F.d
• A força F tem a mesma direção e sentido oposto ao do deslocamento d
(θ = 180º)
τ = -F.d
• A força F é perpendicular ao deslocamento d
(θ = 90º)
τ = 0
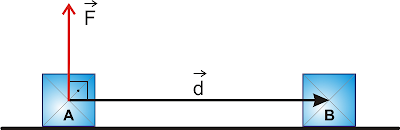
Trabalho do peso
Um bloco sofre um deslocamento d, partindo de uma posição A e chegando a outra B. O trabalho do peso P do bloco no deslocamento d é dado por:
Mas sendo cos θ = h/d, resulta:
τ = P.d.h/d => τ = P.h => τ = m.g.h
Resumindo, para o trabalho do peso, sendo h o desnível entre A e B, temos:
x
τ = +m.g.h: quando o corpo desceτ = -m.g.h: quando o corpo sobe
Observação importante: O trabalho do peso de um corpo entre duas posições A e B independe da trajetória. Depende do peso do corpo e do desnível entre A e B.
Mas qual é o significado físico do trabalho de uma força?
O trabalho de uma força é a medida da energia transferida ou transformada.
Ao ser erguido, a energia potencial gravitacional do bloco aumenta. A energia transferida é medida pelo trabalho da força F que o fio aplica no bloco.
Ao ser abandonado, a energia potencial gravitacional do bloco se transforma em energia cinética. A energia transformada é medida pelo trabalho do peso.
Exercícios básicos:
Exercício 1:
Calcule o trabalho da força constante F de intensidade F = 10 N, num deslocamento d = 2,0 m, nos casos indicados abaixo:
Resolução:
a) τ = F.d.cos 60° => τ = 10.2,0.0,50 => τ = 10 J
b) τ = F.d.cos 0° => τ = 10.2,0.1,0 => τ = 20 J
c) τ = F.d.cos 180° => τ = 10.2,0.(-1,0) => τ = -20 J
d) τ = F.d.cos 90° => τ = 10.2,0.0 => τ = 0
Respostas: a) 10 J; b) 20 J; c) -20 J; d) zero
Exercício 2:
Um pequeno bloco de peso P = 8,0 N, desloca-se numa mesa horizontal passando da posição A para a posição B, sob ação de uma força horizontal F = 10 N. O coeficiente de atrito dinâmico entre o bloco e a mesa é μd = 0,50. Determine os trabalhos das forças, F, Fat, P e FN no deslocamento d = 1,5 m, de A até B.
Resolução:
τ = F.d.cos 0° => τ = 10.1,5.1,0 => τ = 15 J
τ = Fat.d.cos 180° => τ = μd.FN.d.cos 180° => τ = 0,50.8,0.1,5.(-1,0) =>
τ = -6,0 J
τ = P.d.cos 90° => τ = 0
τ = FN.d.cos 90° => τ = 0
Respostas: 15 J; -6 J; zero; zero
Exercício 3:
Calcule o trabalho do peso de um bloco de massa 1,0 kg nos deslocamentos de A até B, segundo as trajetórias (1), (2) e (3). Dados: g = 10 m/s2 e h = 0,5 m.
Resolução:
O trabalho do peso independe da trajetória. Entre os pontos A e B e é dado por:
τ = +m.g.h => τ = +1,0.10.0,5 => τ = +5,0 J
Resposta: +5 J nas três trajetórias
Texto referente aos exercícios 4 e 5.
Uma pequena esfera de peso 1,0 N é lançada obliquamente do ponto A do solo horizontal, com velocidade v0. A altura máxima atingida (ponto B) é h = 2,4 m. O ponto C encontra-se a uma altura h/2 do solo.
Exercício 4:
Calcule o trabalho realizado pelo peso da esfera no deslocamento de A até B.
Resolução:
De A até B o corpo sobe. Logo:
τ = -m.g.h => τ = -1,0.2,4 => τ = -2,4 J
Resposta: -2,4 J
Exercício 5:
Calcule o trabalho realizado pelo peso da esfera no deslocamento de B até C.
Resolução:
De B até C o corpo desce. Logo:
τ = +m.g.(h/2) => τ = +1,0.1,2 => τ = +1,2 J
Resposta: +1,2 J









Nenhum comentário:
Postar um comentário