Cursos do Blog - Eletricidade

Voltando ao segundo fenômeno eletromagnético

Borges e Nicolau

x
Vimos que todo condutor percorrido por corrente elétrica e imerso num campo magnético fica, em geral, sujeito a uma força F_m, denominada força magnética. Este é o segundo fenômeno eletromagnético.

Sendo a corrente elétrica um movimento ordenado de partículas eletrizadas, concluímos que uma partícula eletrizada em movimento num campo magnético fica, em geral, sob ação de uma força magnética.

Vamos dar as características da força magnética F_m que age numa partícula eletrizada com carga elétrica q, lançada com velocidade v num campo magnético uniforme B. Seja θ o ângulo entre B e a velocidade v.

Clique para ampliar

Características da força magnética F_m:

Direção: da reta perpendicular a B e a v

Sentido: determinado pela regra da mão direita número 2. Disponha a mão direita espalmada com os quatro dedos lado a lado e o polegar levantado. Coloque o polegar no sentido da velocidade v e os demais dedos no sentido do vetor B. O sentido da força magnética F_m seria, para q>0, aquele para o qual a mão daria um empurrão. Para q<0, o sentido da força magnética F_m é oposto ao dado pela regra da mão direita número 2.

Clique para ampliar

Observação: O sentido da força magnética pode também ser determinado pela regra da mão esquerda. Os dedos da mão esquerda são dispostos conforme a figura abaixo: o dedo indicador é colocado no sentido de B, o dedo médio no sentido de v. O dedo polegar fornece o sentido de F_m, considerando q>0. Para q<0, o sentido da força magnética F_m é oposto ao dado pela regra da mão esquerda.

Clique para ampliar

Intensidade: a intensidade da força magnética F_m depende do valor q da carga elétrica da partícula, do módulo v da velocidade com que a partícula é lançada, da intensidade do vetor campo magnético B e do ângulo θ entre B e v. É dada por:

CASOS PARTICULARES IMPORTANTES

1. Se v = 0 (partícula abandonada em repouso), resulta F_m = 0.

Portanto, partículas eletrizadas abandonadas em repouso não sofrem ação do campo magnético.

2. Partícula eletrizada lançada paralelamente às linhas de indução de um campo magnético uniforme (v paralelo a B)

Neste caso, θ = 0 ou θ = 180º e sendo sen 0 = 0 e sen 180º = 0, concluímos que a força magnética é nula.

Portanto, a partícula desloca-se livre da ação de forças, realizando um movimento retilíneo e uniforme (MRU).

Clique para ampliar

3. Partícula eletrizada lançada perpendicularmente às linhas de indução de um campo magnético uniforme (v perpendicular a B).

Neste caso, θ = 90º e sendo sen 90º = 1, resulta:

A força magnética é sempre perpendicular à velocidade v. Ela altera a direção da velocidade e não seu módulo. Sendo q, v e B constantes, concluímos que o módulo da força magnética F_m é constante. Logo, a partícula está sob ação de uma força de módulo constante e que em cada instante é perpendicular à velocidade.

Clique para ampliar

Portanto, a partícula realiza movimento circular uniforme (MCU).

Cálculo do raio da trajetória

Seja m a massa da partícula e R o raio da trajetória. Observando que a força magnética é uma resultante centrípeta, vem:

Clique para ampliar

4. Partícula lançada obliquamente às linhas de indução. Neste caso, decompomos  a velocidade de lançamento v nas componentes: v₁ (paralela a B) e v₂ (perpendicular a B). Devido a v₁ a partícula descreve MRU e devido a v₂, MCU. A composição de um MRU com um MCU é um movimento denominado helicoidal. Ele é uniforme.

Clique para ampliar

Exercícios Básicos

Exercício 1:

Represente a força magnética que age na partícula eletrizada com carga elétrica q, nos casos:

Clique para ampliar

Resolução:

Basta aplicar a regra da mão direita número 2 ou a regra da mão esquerda. Não esqueça que para q < 0, o sentido da força magnética F_m é oposto ao dado pelas citadas regras. Assim, temos:

Exercício 2:

Quatro partículas eletrizadas, A, B, C e D, são lançadas num campo magnético uniforme, conforme indica a figura. Qual é a trajetória e o tipo de movimento realizado que cada partícula realiza?

Clique para ampliar

Resolução:

As partículas eletrizadas A e B são lançada paralelamente às linhas de indução do campo magnético uniforme (v paralelo a B).

Nestes casos, a força magnética é nula. Concluímos, então, que  as partículas deslocam-se livres da ação de forças, realizando movimento retilíneo e uniforme (MRU).

A partícula eletrizada C é lançada perpendicularmente às linhas de indução do campo magnético uniforme (v perpendicular a B). Neste caso, a partícula realiza movimento circular uniforme (MCU).

A partícula D é lançada obliquamente às linhas de indução. Ela realiza  um movimento denominado helicoidal uniforme.

Resumindo:

Exercício 3:
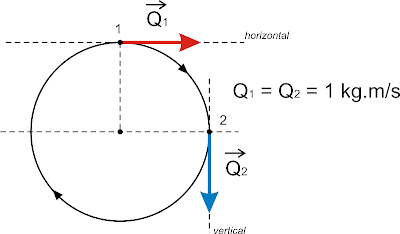
Represente as trajetórias das partículas eletrizadas, (1) e (2). Considere que as partículas não abandonam a região na qual existe o campo magnético uniforme.

Clique para ampliar

Resolução:

Em cada situação determinamos, na posição de lançamento, a força magnética F_m. Esta força aponta para o centro da circunferência que tangencia a velocidade v. Temos:

Exercício 4:
Uma partícula de massa m e eletrizada com carga elétrica q<0 é lançada de um ponto O, com velocidade v = 10⁵ m/s, numa região onde existe um campo magnético uniforme de intensidade B = 10^-3 T. A partícula descreve a semi-circunferência indicada na figura, incidindo no ponto C do anteparo. Sendo q/m = -10⁹ C/kg, calcule a distância do ponto O ao ponto C.

Clique para ampliar

Resolução:

Resposta: 0,2 m

Exercício 5:
Um feixe de partículas constituído de elétrons, nêutrons e pósitrons (elétrons positivos) é lançado num campo magnético uniforme. As partículas descrevem as trajetórias I, II e III, indicadas na figura. Identifique a trajetória dos elétrons, dos nêutrons e dos pósitrons.

Clique para ampliar

Resolução: 

Os nêutrons não ficam sujeitos a forças magnéticas. Logo atravessam o campo sem desvio. Portanto, II é a trajetória dos nêutrons. Aplicando a regra da mão direita número 2, na posição de lançamento, notamos que a força magnética é para baixo, se a partícula tiver carga elétrica positiva, e para cima, se negativa. Logo I é a trajetória dos elétrons e III, dos pósitrons.
Resulta então: I: elétrons; II: nêutrons; III: pósitrons.

Respostas: I: elétrons; II: nêutrons; III: pósitrons

Exercício 6:
Uma partícula de massa m e eletrizada com carga elétrica q é lançada com velocidade v, perpendicularmente às linhas de indução  de um campo magnético uniforme de intensidade B. A partícula descreve uma trajetória circular. Qual é o intervalo de tempo gasto para completar uma volta, isto é, qual é o período do movimento? O período depende da velocidade com que a partícula foi lançada?

Resolução:

v = Δs/Δt => v = 2.π.R/T => T = 2.π.R/v =>
T = (2.π/v).(m.v/B.IqI) => T = 2.π.m/B.IqI

O período não depende da velocidade de lançamento.

Respostas: T = 2.π.m/B.IqI e não depende da velocidade de lançamento.

Cursos do Blog - Termologia, Óptica e Ondas

Equação de Gauss. Aumento linear transversal

Borges e Nicolau

Equação de Gauss

Na aula anterior aprendemos como obter graficamente a imagem de um objeto colocado diante de  uma lente esférica delgada. A posição da imagem pode ser obtida por meio de uma equação: Equação de Gauss. 

Clique para ampliar

Sejam p e p’ as abscissas do objeto e da imagem em relação ao sistema de eixos cartesianos indicado na figura acima, obedecendo à seguinte convenção de sinais:

Objeto real: p > 0
Imagem real: p' > 0
Imagem virtual: p' < 0

Para a distância focal f, temos:

Lente convergente: f > 0
Lente divergente: f < 0

p, p’ e f se relacionam pela Equação de Gauss:

1/f = 1/p + 1/p'

Aumento linear transversal A

Sejam i e o as alturas da imagem e do objeto, respectivamente. A relação entre i e o é indicada por A e recebe o nome de aumento linear transversal:

A = i/o

Convenção de sinais:

Imagem direita: A > 0
Imagem invertida: A < 0

O aumento linear transversal e as abscissas p e p’ do objeto e da imagem também se relacionam:

A = -p'/p

Exercícios básicos

Exercício 1:
Um objeto linear situa-se a 30 cm de uma lente delgada convergente de distância focal 5 cm.

a) Determine a que distância da lente se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.

Resolução:

a) São dados: p = 30 cm e f = 5 cm. Aplicando a equação de Gauss determinamos o valor de p’:

1/f = 1/p + 1/p’ => 1/5 = 1/30 + 1/p’ => 1/p’ = 1/5 -1/30 =>
1/p’ = (6-1)/30 => p’ = +6 cm

A imagem se forma a uma distância de 6 cm da lente.

b) Sendo p’ > 0, concluímos que a imagem é real

c)

Respostas: a) 6 cm; b) real; c) esquema acima

Exercício 2:
Um objeto linear situa-se a 12 cm de uma lente delgada divergente cuja distância focal é, em módulo, igual a 6 cm.

a) Determine a que distância da lente se forma a imagem.
b) A imagem é real ou virtual?
c) Represente a lente, o objeto e utilizando dois raios notáveis obtenha a imagem.

Resolução:

a) São dados: p = 12 cm e f = -6 cm. Aplicando a equação de Gauss determinamos o valor de p’:

1/f = 1/p + 1/p’ => 1/-6 = 1/12 + 1/p’ => 1/p’ = 1/-6 -1/12 =>
1/p’ = (-2-1)/12 => p’ = -4 cm.

A imagem se forma a uma distância de 4 cm da lente.

b) Sendo p’ < 0, concluímos que a imagem é virtual

c)

Respostas: a) 4 cm; b) virtual; c) esquema acima

Exercício 3:
A imagem real de um objeto fornecida por uma lente delgada convergente, de distância focal 30 cm, situa-se a 40 cm da lente. Determine:

a) a que distância da lente está posicionado o objeto;
b) o aumento linear transversal.

Resolução:

a) Sendo p’ = 40 cm e f = 30 cm, calculamos p pela equação de Gauss:

1/f = 1/p + 1/p’ => 1/30 = 1/p + 1/40 => 1/p = 1/30 - 1/40 =>
1/p = (4-3)/120 => p = 120 cm

b) O aumento linear transversal é dado por:

A = -p’/p => A = - 40/120 => A = - 1/3 => a imagem é invertida e tem altura igual a um terço da altura do objeto.

Respostas: a) 120 cm; b) -1/3

Exercício 4:
A imagem de um objeto situado diante de uma lente delgada divergente tem altura 3 vezes menor do que a do objeto. O módulo da distância focal da lente é de 15 cm. Determine a distância entre o objeto e a imagem.

Resolução:

Sendo a lente divergente, temos: f = -15 cm.
A imagem é direita. Logo: i = o/3
 
A = i/o = -p’/p => A = (o/3)/o = -p’/p => 1/3 = -p’/p => p’ = -p/3 (1)
 
Equação de Gauss: 1/f = 1/p + 1/p’=> 1/-15 = 1/p + -3/p => p = 30 cm
 
De (1), vem: p’ = -10 cm.
 
O objeto está a 30 cm diante da lente.
A imagem está diante da lente e a 10 cm.
Logo a distância entre o objeto e a imagem é de 20 cm

Resposta: 20 cm

Exercício 5:
Dois objetos retilíneos de mesma altura, O₁ e O₂, são dispostos perpendicularmente ao eixo principal de uma lente delgada convergente, conforme indica a figura. A e A’ são os pontos anti-principais objeto e imagem; F e F’ os focos principais objeto e imagem. Determine:

a) a distância entre as imagens conjugadas.
b) a relação entre as alturas i₁ e i₂ das imagens de O₁ e O₂, respectivamente.

  
Resolução:

a) Imagem de O₁
 
1/f = 1/p + 1/p’ => 1/10 = 1/30 + 1/p’ => 1/p’ = 1/10 -1/30 =>
1/p’ = (3-1)/30 => p’ = 15 cm

Imagem de O₂
 
1/f = 1/p + 1/p’ => 1/10 = 1/20 + 1/p’ => 1/p’ = 1/10 -1/20 =>
1/p’ = (2-1)/20 => p’ = 20 cm
 
A distância entre as duas imagens é igual a: 20 cm – 15 cm = 5 cm

b) Vamos aplicar duas vezes a relação; i/o = -p’/p

i₁/o = - 15/30 => i₁/o = -1/2 (1) 
i₂/o = - 20/20 => i₂/o = -1 (2)

De (1) e (2), vem: i₁/i₂ = 1/2

Respostas: a) 5 cm; b) i₁/i₂ = 1/2

Cursos do Blog - Mecânica

Impulso e Quantidade de Movimento

Borges e Nicolau

Um corpo de massa m desloca-se com velocidade vetorial constante v₁. Num certo instante t₁ uma força resultante F, constante, passa a agir no corpo, na direção e sentido de v₁. Nestas condições, num instante t₂ a velocidade vetorial do corpo passa a ser v₂.

Pela Segunda Lei de Newton, temos:
  

F = m.a
 

Sendo F constante, resulta que a aceleração a é também constante e podemos escrever: a = Δv/Δt. Assim, temos:
F = m.Δv/Δt
F.Δt = m.(v₂ - v₁)
F.Δt = m.v₂ - m.v₁ (1)

Este resultado introduz dois novos conceitos:

• o de impulso I de uma força constante F que age num corpo num intervalo de tempo Δt: I = F.Δt.

O impulso I tem a mesma direção e sentido da força constante F.
Sua intensidade I = F.Δt é medida no SI em newton x segundo (N.s).

• o de quantidade de movimento Q igual ao produto da massa m do corpo pela sua velocidade vetorial v: Q = m.v.

A quantidade de movimento Q tem a mesma direção e o mesmo sentido da velocidade vetorial v.
Sua intensidade Q = m.v é medida no SI em quilograma x metro por segundo (kg.m/s). 

Assim, nos instantes t₁ e t₂, temos:

Q₁= m.v₁ e Q₂= m.v₂

De (1), levando em conta os conceitos definidos, obtemos:

I = Q₂- Q₁

                                                     
Este último resultado constitui o Teorema do Impulso: O impulso da força resultante num dado intervalo de tempo é igual à variação da quantidade de movimento no mesmo intervalo de tempo.
Este teorema tem validade geral, embora tenha sido demonstrado no caso em que a força resultante é constante.

Observação: Se a força F tiver direção constante e intensidade variável em função do tempo, a intensidade do impulso da força, num certo intervalo de tempo, é numericamente igual à área no diagrama F x t:

Recorde os conceitos de Impulso e Quantidade de Movimento por meio de animações.                                                                                                    
Clique aqui e aqui

Exercícios básicos

Exercício 1:
Uma força horizontal, para a direita, com intensidade constante F = 10 N, age num bloco durante um intervalo de tempo de 10 s. Dê a direção, o sentido e a intensidade do impulso da força no intervalo de tempo considerado.

Resolução:

direção: horizontal, isto é, a mesma direção da força.
sentido: para a direita, isto é, o mesmo sentido da força.
intensidade: I = F.Δt => I = 10 N.10 s => I = 100 N.s

Respostas:
direção: horizontal
sentido: para a direita
intensidade: I = 100 N.s

Exercício 2:
Uma pequena esfera cujo peso tem intensidade 2,0 N é abandonada de  uma certa altura e atinge o solo depois de 6,5 s. Dê a direção, o sentido e a intensidade do impulso do peso da esfera desde o instante em que foi abandonada até o instante que atinge o solo.

Resolução:

direção: vertical, isto é, a mesma direção do peso da esfera.
sentido: para baixo, isto é, o mesmo sentido do peso da esfera.
intensidade: I = P.Δt => I = 2,0 N.6.5 s => I = 13 N.s

Respostas:
direção: vertical
sentido: para baixo
intensidade: I = 13 N.s

Exercício 3:
Uma pequena esfera de massa m = 0,2 kg descreve, num plano vertical, um movimento circular e uniforme no sentido horário com velocidade escalar de 5 m/s. Represente as quantidades de movimento Q₁ e Q₂ nos instantes em que a esfera passa pelos pontos 1 e 2 indicados na figura e calcule seus módulos.

Resolução:

A direção e o sentido da quantidade de movimento são os mesmos da velocidade vetorial em cada instante. Assim, temos:

Sendo o movimento circular e uniforme a velocidade tem módulo constante o mesmo acontecendo com a quantidade de movimento.

Portanto:

Q₁ = Q₂ = m.v => Q₁ = Q₂ = 0,2 kg.5 m/s = > Q₁ = Q₂ = 1 kg.m/s

Respostas:

Exercício 4:
Retome o exercício anterior. Represente o vetor Q₂ - Q₁ e calcule o seu módulo.

Resolução: 

Representação do vetor Q₂ - Q₁

O módulo do vetor Q₂ - Q₁ é a diagonal do quadrado de lado 1 kg.m/s, portanto igual a 1.√2 kg.m/s = √2 kg.m/s

Respostas:

Exercício 5:
Um corpo se desloca sob ação de uma força de direção constante. Qual é a intensidade do impulso que age no corpo no intervalo de tempo de 0 a 10 s?
Considere os casos:

Nota: As notações de força (F), velocidade (v), impulso (I) e quantidade de movimento (Q), em negrito, representam grandezas vetoriais.

Resolução:

Vimos que se a força F tiver direção constante e intensidade variável em função do tempo, a intensidade do impulso da força, num certo intervalo de tempo, é numericamente igual à área no diagrama F x t. Assim, temos:

a) I = área do trapézio =>
(base maior + base menor).altura/2 = (10 +5).10/2 => I = 75 N.s
b) I = área do triângulo => 
base.altura/2 = 10.10/2 => I = 50 N.s

Respostas: a) 75 N.s; b) 50 N.s

Arte do Blog

 Two Woman Drinking Coffee

Edouard Vuillard

Édouard Vuillard nasceu em Cuiseaux em 11 de novembro de 1868. Após a morte de seu pai, em 1883, sua mãe montou uma oficina de costura em Paris, no apartamento onde foram morar. Ela foi a maior incentivadora de ambições artísticas em Vuillard. Apesar de conhecido e respeitado Édouard levou uma vida monótona e nunca se casou.

Children in a Room

Em 1889 Vuillard começou a trabalhar na Académie Julian, onde conheceu Maurice Denis, Pierre Bonnard, Paul Ranson, e Paulo Sérusier. Este foi o núcleo do grupo Nabi (profeta em hebreu).

 The Peabody Opera Workshop presents two French...

Muitos de seus trabalhos iniciais são modestas em tamanho e foram considerados "ilegível" em seus matizes rarefeitos. Foram os grandes painéis decorativos que mostraram a arte de Vuillard em todo o seu potencial, obtendo notável aceitação popular.

 Portrait of Madame Hessel

Em 1890 Édouard fez seu primeiro programa de teatro para o Théâtre Libre, uma arte que aperfeiçoou ao colaborar com o Théâtre l'Oeuvre, que ele ajudou a fundar a partir de 1893, e onde trabalhou até 1898. Após a virada do século a arte Vuillard perdeu muito de sua originalidade e força. Ele sempre foi um pintor habilidoso, no entanto, em seus retratos de membros das classes superiores já não há inquietação criativa, mas são extraordinários pelo interesse nas minúcias dos arredores.

 Les couturières

Em 1937 Vuillard fez projetos decorativos para o Palais de Chaillot e, em 1938, para a Liga das Nações Palace de Genebra. Em 1938 ele foi homenageado com uma grande exposição retrospectiva no Musée des Arts Décoratifs e foi eleito para a Academia de Belas Artes.  

Edouard Vuillard morreu em La Baule em 21 de junho de 1940.

Saiba mais aqui e aqui