Cinemática

Clique para ampliar

Movimento circular uniforme (Introdução)

Borges e Nicolau

Quando um ponto material percorre uma trajetória circular com velocidade escalar constante, dizemos que ele realiza um movimento circular e uniforme. (MCU) Podemos estudar o movimento circular relacionando arcos de circunferência e os ângulos centrais correspondentes. A grandeza que utilizaremos para medir os ângulos é o radiano (rad).

Radiano

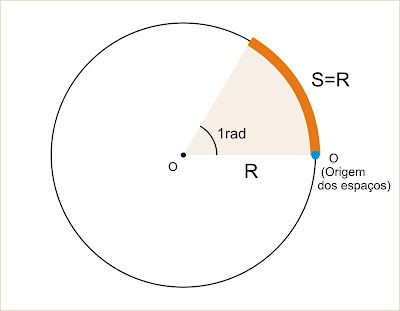
Ângulo central de 1 radiano (1rad) é aquele que determina na circunferência um arco S de comprimento igual ao do raio R.

ângulo centralxxxxarco

1xxxxxxxxxxxxxxR

φxxxxxxxxxxxxxxS

S = φ.R

Um arco qualquer tem medida igual ao produto do ângulo central correspondente, em radianos, pelo raio da circunferência.

Clique para ampliar

Na figura acima um ponto material vai da origem O ao ponto P descrevendo o arco S. O ângulo central correspondente é φ. Podemos escrever:

S = φ.R

onde:

xxxxxxxxxxxxxxS = Espaço linear (medido em metros)

xxxxxxxxxxxxxxφ = Espaço angular (medido em radianos)

xxxxxxxxxxxxxxR = Raio da circunferência (medido em metros)

Considere um ponto material realizando um movimento circular uniforme (MCU) de raio R. Sejam S1 e S2 os espaços lineares do ponto nos instantes t1 e t2 e φ1 e φ2 os correspondentes ângulos centrais:

S1 = φ1.R e S2 = φ2.R

Variação do espaço linear:           ΔS = S2 - S1

ΔS = φ2.R - φ1.R

ΔS = Δφ.R

Dividindo-se ambos os membros por Dt = t2 - t1, resulta:
 

ΔS/Δt = Δφ/Δt . R

Sendo v = ΔS/Δt (velocidade linear) e ω = Δφ/Δt (velocidade angular), vem:

v = ω . R

Para Δφ = 2πrad e Δt = T, resulta: ω = 2π/T