Universidade Federal do Rio de Janeiro
Resoluções fornecidas pela UFRJ
Questão 1
Um avião vai decolar em uma pista retilínea. Ele inicia seu movimento na cabeceira da pista com velocidade nula e corre por ela com aceleração média de 2,0 m/s2 até o instante em que levanta voo, com uma velocidade de 80 m/s, antes de terminar a pista.
a) Calcule quanto tempo o avião permanece na pista desde o início do movimento até o instante em que levanta voo.
b) Determine o menor comprimento possível dessa pista.
Resolução:
a) Como, por definição, am = Δv/Δt, temos Δt = Δv/am. Substituindo os valores do enunciado, obtemos Δt = (80m/s) ⁄ (2,0m/s2), ou seja, Δt = 40s.
b) Na situação em que a pista tem o comprimento mínimo (dm), o avião perde o contato com a pista exatamente em seu final. Com isso, usando a equação de Torricelli, v2 – v02 = 2amΔs, obtemos (80)2 = 2 × 2,0 × dm, donde dm = 1600m.
********************
Questão 2
A figura a seguir (evidentemente fora de escala) mostra o ponto O em que está o olho de um observador da Terra olhando um eclipse solar total, isto é, aquele no qual a Lua impede toda luz do Sol de chegar ao observador.
Clique para ampliar
a) Para que o eclipse seja anelar, isto é, para que a Lua impeça a visão dos raios emitidos por uma parte central do Sol, mas permita a visão da luz emitida pelo restante do Sol, a Lua deve estar mais próxima ou mais afastada do observador do que na situação da figura? Justifique sua resposta com palavras ou com um desenho.
b) Sabendo que o raio do Sol é 0,70 × 106 km, o da Lua, 1,75 × 103 km, e que a distância entre o centro do Sol e o observador na Terra é de 150 × 106 km, calcule a distância d entre o observador e o centro da Lua para a qual ocorre o eclipse total indicado na figura.
Resolução:
a) A Lua deve se afastar da Terra de modo que os raios emitidos pelo Sol dentro dos ângulos AOA’ e BOB’, indicados na figura a seguir, atinjam o ponto O enquanto os raios emitidos dentro do ângulo A’OB’ continuem bloqueados pela Lua.
Clique para ampliar
Clique para ampliar
********************
Questão 3
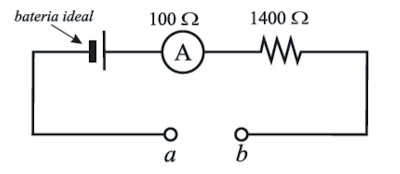
Uma bateria ideal, um amperímetro de resistência interna de 100 Ω e um resistor de resistência de 1400 Ω são ligados em série em um circuito inicialmente aberto com terminais a e b, como indicado na figura a seguir.
Clique para ampliar
Quando os terminais a e b são conectados por um fio de resistência desprezível, fechando o circuito, se estabelece no amperímetro uma corrente de 1,00mA. Quando os terminais a e b são conectados por um resistor, fechando o circuito, se estabelece no amperímetro uma corrente de 0,20mA.
Calcule a resistência desse resistor.
Resolução:
A mesma fem (da bateria ideal) gera uma corrente de 1,00mA quando a resistência total é 100Ω + 1400Ω e uma corrente de 0,20mA quando a resistência total é 100Ω + 1400Ω + R.
Portanto, 1,5 = (1500 + R)×0,20×10-3, donde 1500 = (1500 + R)×0,20, donde R = 7500 - 1500, isto é, R = 6,0×103Ω.
********************
Questão 4
Um brinquedo muito divertido é o telefone de latas. Ele é feito com duas latas abertas e um barbante que tem suas extremidades presas às bases das latas. Para utilizá-lo, é necessário que uma pessoa fale na “boca” de uma das latas e uma outra pessoa ponha seu ouvido na “boca” da outra lata, mantendo os fios esticados.
Como no caso do telefone comum, também existe um comprimento de onda máximo em que o telefone de latas transmite bem a onda sonora.
Clique para ampliar
Sabendo que para um certo telefone de latas o comprimento de onda máximo é 50cm e que a velocidade do som no ar é igual a 340m/s, calcule a frequência mínima das ondas sonoras que são bem transmitidas pelo telefone.
Resolução:
Como a velocidade da onda é o produto de seu comprimento de onda por sua frequência, a frequência mínima para uma boa transmissão é a razão entre a velocidade de propagação da onda e o comprimento de onda máximo para boa transmissão, isto é, fmin = (340m/s)/0,50m, ou seja, fmin = 680Hz.
********************
Questão 5
Inicialmente, um barquinho flutua em repouso na superfície da água contida em um balde, como ilustra a figura 1. Então, um pouco da água do balde é transferida suavemente para dentro do barquinho (figura 2) que, finalmente, volta ao repouso ainda flutuando na superfície da água (figura 3). Tanto na situação inicial, quanto na final, a água do balde está em equilíbrio hidrostático.
Clique para ampliar
Indique se o nível da água no balde na situação final é menor, igual ou maior do que o nível na situação inicial. Justifique sua resposta.
Resolução:
Tanto antes quanto depois de a água ser colocada no interior do barquinho, o módulo do empuxo sobre o sistema é igual ao módulo do peso do sistema: Ei = Pi e Ef = Pf onde i significa situação inicial e f, situação final. Subtraindo a primeira equação da segunda, obtemos a variação do empuxo Ef – Ei = Pf – Pi, ou seja, E = mag = ρagVa, onde ρa é a densidade volumar da água e Va, o volume da quantidade de água inserida no barquinho. Uma vez que E = ρagVd, onde Vd é o aumento no volume de água deslocada pelo barquinho, concluímos que Vd = Va, o que nos permite afirmar que o nível da superfície livre da água no balde permanecerá o mesmo.
********************
Questão 6
Um bloco de massa 2,0 kg está sobre a superfície de um plano inclinado, que está em movimento retilíneo para a direita, com aceleração de 2,0 m/s2, também para a direita, como indica a figura a seguir. A inclinação do plano é de 30º em relação à horizontal.
Clique para ampliar
Suponha que o bloco não deslize sobre o plano inclinado e que a aceleração da gravidade seja g = 10 m/s2.
Usando a aproximação √3 ≈ 1,7 , calcule o módulo e indique a direção e o sentido da força de atrito exercida pelo plano inclinado sobre o bloco.
Resolução:
Suponha que a força de atrito, fat, esteja orientada como na figura.
Clique para ampliar
Uma vez que o corpo se move com aceleração horizontal para a direita de módulo igual a 2,0m/s2, a força resultante que atua sobre o bloco é horizontal, para a direita e tem módulo igual a 4,0N. Decompondo as forças ao longo dos eixos horizontal e vertical (orientados para a direita e para cima, respectivamente) e usando os valores cos30º = √3/2 e sen30º = 1/2, podemos escrever: –fat √3/2 + N/2 = 4 e –20 + N√3/2 + fat /2 = 0. Multiplicando a primeira equação por √3 e subtraindo o resultado da segunda, obtemos 2 fat = –4√3 + 20. Usando a aproximação √3 ≈ 1,7, obtemos
fat = (–6,8 + 20)/2 , ou seja, fat = 6,6N.
Como o valor obtido para fat foi positivo, o sentido suposto para é o correto. Logo, a direção de é paralela ao plano inclinado e seu sentido é de subida.
********************
Questão 7
Um físico alpinista escalou uma alta montanha e verificou que, no topo, a pressão p do ar era igual a 0,44po , sendo po a pressão ao nível do mar. Ele notou também que, no topo, a temperatura T era igual a 0,88To , sendo To a correspondente temperatura ao nível do mar, ambas temperaturas medidas em Kelvin.
Considerando o ar no topo e ao nível do mar como um mesmo gás ideal, calcule a razão d / do entre a densidade d do ar no topo da montanha e a correspondente densidade do ao nível do mar.
Resolução:
Considerando uma mesma massa M do gás ideal no nível do mar e no topo da montanha, poVo/To=pV/T. Dividindo ambos os membros dessa equação por M e fazendo as identificações Vo/M = 1/do e V/M = 1/d, sendo do e d as respectivas densidades volumares do gás no nível do mar e no topo da montanha, temos po / (To do) = p / (Td), donde d/do = (p/po)(To/T) = 0,44/0,88, isto é, d/do = 1/2.
********************
Questão 8
Um íon de massa m e carga elétrica q incide sobre um segundo íon, de mesma massa m e mesma carga q. De início, enquanto a separação entre eles é grande o bastante para que as forças mútuas sejam desprezíveis, o primeiro mantém uma velocidade constante de módulo vo e o segundo se mantém em repouso, como indica a figura 1.
Clique para ampliar
Ao se aproximarem, as forças elétricas coulombianas entre eles, não mais desprezíveis, passam a mudar continuamente suas velocidades. Despreze quaisquer outras forças, considere dados os valores de m, q, vo e 4πεo e suponha que todos os movimentos se deem em uma reta.
a) Calcule a velocidade do segundo íon quando a velocidade do íon incidente for igual a 3vo /4 (como indicado na figura 2).
b) Calcule a distância entre eles no instante da situação considerada no item anterior.
Resolução:
a) Como não há forças externas sobre o sistema, há conservação do seu momento linear, de modo que mvo=m(3vo/4)+mv’, donde v’=vo/4.
b) Como as forças sobre o sistema são conservativas, há conservação da energia mecânica. Assim, (1/2)mvo2 = (1/2)m(3vo/4)2 + (1/2)m(vo/4)2 + (q2/4πεo) (1/d), donde (6/16) mvo2 = (q2/2πεo) (1/d), donde
d = (4q2/3πεomvo2)
********************
Questão 9
Um portão retangular de massa igual a 50kg tem 2,50m de comprimento, 1,45m de altura e está preso a duas dobradiças A e B. O vértice da dobradiça A dista 0,10m do topo do portão, e o vértice da dobradiça B, 0,10m da base, como indica a figura a seguir.
Clique para ampliar
Suponha que o sistema esteja em repouso, que o peso do portão esteja aplicado em seu centro geométrico e que a aceleração g da gravidade local seja 10m/s2.
a) Calcule o módulo da força resultante exercida pelas duas dobradiças sobre o portão.
b) Calcule o módulo da componente horizontal da força exercida pela dobradiça A sobre o portão e determine seu sentido.
Resolução:
a) As forças que atuam no portão são o peso P, a força FA do apoio A e a força FB do apoio B. Como o sistema está em equilíbrio, FA + FB + P = 0, donde IFA + FBI = P = 50kg×10m/s2, isto é, IFA + FBI= 500N.
b) Para calcular o módulo FAh da força horizontal FA, usamos o fato de que é nulo o torque das forças relativo ao ponto B. Para que isso ocorra, a componente horizontal de FA deve apontar para a esquerda e satisfazer a relação FAh×1,25 – 500×1,25=0, donde FAh = 500N.
********************
Questão 10
Uma partícula de massa m e carga q positiva, em movimento retilíneo uniforme, penetra em uma região na qual há um campo magnético uniforme, vertical e de módulo B. Ao sair da região, ela retoma um movimento retilíneo uniforme.
Todo o movimento se processa em um plano horizontal e a direção do movimento retilíneo final faz um ângulo θ com a direção do movimento retilíneo inicial. A velocidade da partícula é grande o bastante para desprezarmos a força gravitacional, de modo a considerarmos apenas a força magnética sobre ela.
Clique para ampliar
a) Determine a razão v’ / v entre o módulo v’ da velocidade do movimento retilíneo final e o módulo v da velocidade do movimento retilíneo inicial.
b) Calcule quanto tempo a partícula demora para atravessar a região em que há campo magnético em função de q, m, B e θ.
Resolução:
a) Como a força magnética não realiza trabalho, a energia cinética da partícula não muda. Portanto, não se altera o módulo de sua velocidade e, consequentemente, v’/v=1.
b) O movimento da partícula no campo magnético é circular uniforme com velocidade de módulo v e raio R tais que, pela segunda lei de Newton, qvB = m(v2/R), ou seja, m(v/R) = qB. Lembrando que a velocidade angular da partícula é ω = v/R, obtemos ω = qB/m. Usando esse resultado na expressão t = θ/ ω , que dá o tempo t que a partícula demora para atravessar a região, obtemos t = mθ/(qB).










Nenhum comentário:
Postar um comentário