9ª aula
Movimento vertical no vácuo
Borges e Nicolau
Movimento vertical no vácuo
Borges e Nicolau
x
O movimento vertical no vácuo é um caso particular de movimento uniformemente variado (MUV).A aceleração α é igual à aceleração da gravidade g.
Um móvel lançado verticalmente para cima, no vácuo, descreve um movimento uniformemente variado retardado, atingindo a altura máxima quando sua velocidade escalar, cujo módulo decresce com o tempo, torna-se igual a zero.
Ao descer, a velocidade escalar do móvel aumenta em módulo, o movimento é acelerado. A velocidade com que o móvel atinge o solo é, em módulo, igual à velocidade de lançamento. O tempo de subida é igual ao tempo de descida.
Animação:
Movimento vertical no vácuo
Clique aqui
Exercícios Básicos
Exercício 1:
Na superfície terrestre a aceleração da gravidade “g” tem um valor próximo
de 10 m/s2. Na prática isso significa que a velocidade de um corpo abandonado em queda livre, aumenta 10 m/s a cada segundo. Ou seja, no primeiro segundo o corpo atinge 10 m/s, depois, em intervalos de um segundo, 20 m/s, 30 m/s, 40 m/s, 50 m/s e assim por diante.
Em 5 segundos de queda, portanto, a velocidade é igual a
50 m/s = (50 x 3,6) km/h = 180 km/h.
Você sabe que quando a aceleração é constante, o movimento é uniformemente variado. (MUV)
Calcule:
a) a altura da qual um corpo partiu do repouso e atingiu o solo com
velocidade de 50 m/s;
b) o tempo de queda.
Resolução: clique aqui
a) Adotando-se a origem no ponto de partida e orientando-se a trajetória para baixo, temos de acordo com a equação de Torricelli:
v2 = (v0)2 + 2.g.Δs => (50)2 = 2.10.H => H = 125 m
b) s = (g.t2)/2 => H = (g.tq2)/2 => tq = √(2.H/g) => tq = √(2.125/10) => tq = 5 s
Respostas:
a) H = 125 m
b) t = 5 s
Exercício 2:
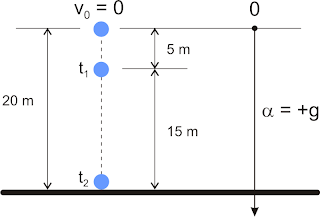
Uma pedra é abandonada de uma altura igual a 20 m. Determine o intervalo de tempo decorrido para a pedra percorrer os últimos 15 m de queda. Considere
g = 10 m/s2 e despreze a resistência do ar.
Resolução: clique aqui
s = (g.t2)/2 => 5 = (10.t12)/2 => t1 = 1 s
s = (g.t2)/2 => 20 = (10.t22)/2 => t2 = 2 s
Δt = t2 - t1 = 2 s - 1 s = 1 s
Resposta: Δt = 1 s
Exercício 3:
Você faz uma pequena bolinha de papel e a lança verticalmente para cima com velocidade de 5 m/s. Quanto tempo a bolinha demora para voltar à sua mão. Qual é a altura máxima atingida pela bolinha. Considere g = 10 m/s2 e despreze a resistência do ar.
Resolução: clique aqui
Vamos calcular o tempo de subida (ts)
v = v0 - g.t => 0 = v0 - g.ts => ts = v0/g => ts = 5/10 => ts = 0,5 s
O tempo de descida é igual ao tempo de subida:
td = ts = 0,5 s
Tempo total:
t = ts + td = 1s
Equação de Torricelli:
v2 = (v0)2 + 2.g.Δs => (5)2 = 2.10.H => H = 1,25 m
Resposta: t = 1 s; H = 1,25 m
Exercício 4:
Uma bolinha é abandonada de uma altura H e percorre no último segundo de queda a distância 3H/4. Despreze a resistência do ar e adote g = 10 m/s2. Determine o valor de H.
Resolução: clique aqui
s = (g.t2)/2 => H/4 = [g.(tq-1)2]/2 (1)
s = (g.t2)/2 => H = (g.tq2)/2 (2)
(2) ÷ (1) => 4 = tq2/(tq-1)2 => 2 = tq/(tq-1) => tq = 2 s
De (2), vem: H = 20 m
Resposta: H = 20 m
Exercício 5:
De uma altura igual a 40 m lança-se verticalmente para baixo uma bolinha com velocidade 10 m/s. Depois de 1 s, lança-se do mesmo ponto, também verticalmente para baixo, outra bolinha com a mesma velocidade inicial da primeira. Qual é a distância entre elas no instante que a primeira bolinha atinge o solo? Despreze a resistência do ar e considere g = 10 m/s2.
Resolução: clique aqui
Vamos determinar o instante em que a primeira bolinha (A) atinge o solo.
s = s0 + v0.t + (1/2).g.t2 => 40 = 0 + 10.t + 5.t2 => t = 2 s
Como a bolinha B foi lançada 1 s depois, devemos achar o espaço ocupado por ela no instante 2 s - 1 s = 1 s:
s = s0 + v0.t + (1/2).g.t2 => s = 0 + 10.1 + 5.(1)2 => s = 15 m.
Assim, a distância entre as bolinhas é de 40 m - 15 m = 25 m
Resposta: d = 25 m
Exercício 6:
Um helicóptero sobe verticalmente em movimento uniforme e com velocidade 10 m/s. Ao atingir a altura de 75 m um pequeno parafuso desprende-se do helicóptero. Quanto tempo o parafuso leva para atingir o solo? Despreze a resistência do ar e adote g = 10 m/s2.
Resolução: clique aqui
Vamos adotar:
Origem dos tempos: instante em que o parafuso se desprende
Origem dos espaços: posição em que o parafuso de desprende
Orientação da trajetória para baixo.
Observe que a velocidade inicial do parafuso é a própria velocidade do helicóptero. Como orientamos a trajetória para baixo, temos v0 = -10 m/s.
s = s0 + v0.t + (1/2).g.t2 = 75 = 0 – 10.t +5.t2 => t = 5 s
Resposta: t = 5 s
Exercícios de revisão
Revisão/Ex1:
(Vunesp)
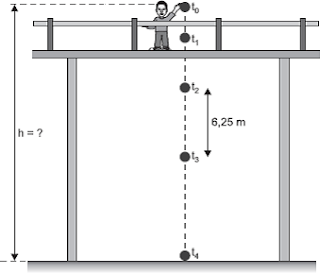
Em um dia de calmaria, um garoto1sobre uma ponte deixa cair, verticalmente e a partir do repouso, uma bola no instante t0 = 0 s. A bola atinge, no instante t4, um ponto localizado no nível das águas do1rio e a distância h do ponto de lançamento. A figura apresenta, fora de escala, cinco1posições da bola, relativas aos instantes t0, t1, t2, t3 e t4. Sabe-se que entre os instantes t2 e t3 a bola percorre 6,25 m e que gx=x10xm/s2.
Desprezando a resistência do ar e sabendo que o intervalo de tempo entre duas posições consecutivas apresentadas na figura é sempre o mesmo, pode-se afirmar que a distância h, em metros, é igual a
a) 25. b) 28. c) 22. d) 30. e) 20.
Resolução: clique aqui
Vamos indicar os instantes t1, t2, t3 e t4 respectivamente por T, 2T, 3T e 4T
s3 – s2 = g. (3T)2/2 – g.(2T)2/2 => 6,25 = 5.g.T2/2 => g.T2/2 = 6,25/5 (1)
h = g.(4T)2/2 => h = 16.g.T2/2
De (1), vem: h = 16. 6,25/5 => h = 20 m.
Resposta: e
Revisão/Ex2:
(UFscar)
Em julho de 2009 comemoramos os 40 anos da primeira viagem tripulada à Lua. Suponha que você é um astronauta e que, chegando à superfície lunar, resolva fazer algumas brincadeiras para testar seus conhecimentos de Física.
a) Você lança uma pequena bolinha, verticalmente para cima, com velocidade v0 igual a 8 m/s. Calcule a altura máxima h atingida pela bolinha, medida a partir da altura do lançamento, e o intervalo de tempo Δt que ela demora para subir e descer, retornando à altura inicial.
b) Na Terra, você havia soltado de uma mesma altura inicial um martelo e uma pena, tendo observado que o martelo alcançava primeiro o solo. Decide então fazer o mesmo experimento na superície da Lua, imitando o astronauta David Randolph Scott durante a missão Apolo 15, em 1971. O resultado é o mesmo que o observado na Terra? Explique o porquê.
Dados:
- Considere a aceleração da gravidade na Lua como sendo 1,6 m/s2.
- Nos seua cálculos mantenha somente 1 (uma) casa depois da vírgula.
Resolução: clique aqui
a) Adotando-se a origem dos espaços no ponto de lançamento e orientando-se a trajetória para cima, temos:
v2 = (v0)2 + 2.(-g).Δs
Ao atingir altura máxima h, a velocidade da bolinha é nula. Portanto:
02 = (v0)2 + 2.(-g).h => 0 = (8)2 - 2.1,6.h => h = 20 m
O tempo de subida ts é calculado fazendo v = 0 na equação da velocidade:
v = v0 - g.t => 0 = 8 - 1,6.ts => ts = 5,0 s
O tempo de descida td é igual ao tempo de subida: td = 5,0 s.
O tempo total é a soma dos tempos de subida e de descida:
ttotal = 5,0 s + 5,0 s = 10 s
b) Na Terra, existe a força de resistência do ar que afeta mais o movimento da pena (mais leve) e por isso o martelo atinge o solo antes.
Como na Lua não há atmosfera, a pena e o martelo caem com aceleração igual à da gravidade lunar e atingem o solo no mesmo instante.
Respostas: a) 20 m; 10 s
Revisão/Ex 3:
(ITA-SP)
Um elevador está descendo com velocidade constante. Durante este movimento, uma lâmpada, que o iluminava, desprende-se do teto e cai. Considere g = 9,8 m/s2. Sabendo-se que o teto está a 3,0 m de altura acima do piso do elevador, o tempo que a lâmpada demora para atingir o piso é:
a) 0,61 s.
b) 0,78 s.
c) 1,54 s.
d) Infinito, pois a lâmpada só atingirá o piso se o elevador sofrer uma desaceleração.
e) Indeterminado, pois não se conhece a velocidade do elevador.
Resolução: clique aqui
A lâmpada cai em MUV. Sua velocidade inicial é a mesma do elevador. O piso sobe em MU.
Lâmpada:
SL = h + v.t - g.t2/2
Piso:
SP = v.t
Encontro:
SL = SP
h + v.t - g.t2/2 = v.t => h - g.t2/2 = 0 => t = √(2.h/g) =>
t = √(2.3,0/9,8) => t ≅ 0,78 s
Resposta: b
Revisão/Ex 4:
(UECE)
Uma pedra cai de uma altura H, a partir0do repouso. No mesmo instante, uma segunda pedra é lançada, do chão, verticalmente para cima com velocidade v0. Desprezando a resistência do ar e supondo0constante a aceleração da gravidade no local da experiência, o valor de v0, para que uma pedra passe pela outra a uma altura H/2, é igual a:
a) 1/2√(gh)
b) √(gh)
c) 1/2√(2gh)
d) √(2gh)
Resolução: clique aqui
Pedra P1: s1 = H-gt2/2
Pedra P1: s2 = v0.t-gt2/2
Encontro: H-gt2/2 = v0.t-gt2/2 => H = v0.t (1)
Mas no encontro s1 = H/2 => H-gt2/2 = H/2 => gt2/2 = H/2
=> t = √(H/g) (2)
(2) em (1): H = v0.√(H/g) => v0 = √(g.H)
Resposta: b
Revisão/Ex 5:
(UFU-MG)
Duas pedras são abandonadas do repouso, ambas de uma altura de 20 m, porém uma na Terra e outra em Marte. Após 1 s ela são observadas nas posições indicadas abaixo.
Considerando gTerra = 10 m/s2 e gMarte = gTerra/3, marque para as alternativas abaixo (V) Verdadeira, (F) Falsa ou (SO) Sem Opção.
1 ( ) O planeta A corresponde à Terra e o planeta B corresponde a Marte.
2 ( ) O módulo da velocidade da partícula em Marte, 3 s após ser abandonada, é 30 m/s.
3 ( ) A pedra abandonada na Terra percorreu uma distância de 20 m após 2 s de queda.
4 ( ) Para que a pedra abandonada em Marte adquira uma mesma velocidade da abandonada na Terra, a pedra em Marte deve percorrer uma distância três vezes maior que a distância percorrida pela pedra na Terra.
Resolução: clique aqui
1. (V)
No Planeta A, temos:
s = s0 + v0.t + (-g).t2/2 => 15 = 20 + 0 + (-g).12/2 => g = 10 m/s2No Planeta A, temos:
2. (F)
v = v0 + (gTerra/3).t => v = 0 + (-10/3).3 => v = - 10 m/s => IvI = 10 m/s
3. (V)
No instante t = 0, temos: s0 = 20 m
Para t = 2 s, temos:
3. (V)
No instante t = 0, temos: s0 = 20 m
Para t = 2 s, temos:
s = s0 + v0.t + (-g).t2/2 => s = 20 + 0 + (-10).22/2 => s = 0
A variação de espaço, no intervalo de 0 a 2 s, foi s - s0 = 0 - 20 m = -20 m e a distância percorrida foi d = 20 m.
A variação de espaço, no intervalo de 0 a 2 s, foi s - s0 = 0 - 20 m = -20 m e a distância percorrida foi d = 20 m.
4. (V)
Vamos aplicar a equação de Torricelli para a queda da pedra em cada planeta. Lembre que v0 = 0 e que Δs = -d (ver item anterior).
Terra: v2 = (v0)2 + 2.(-g).Δs => (vTerra)2 = 0 + 2.gTerra.dTerra
Vamos aplicar a equação de Torricelli para a queda da pedra em cada planeta. Lembre que v0 = 0 e que Δs = -d (ver item anterior).
Terra: v2 = (v0)2 + 2.(-g).Δs => (vTerra)2 = 0 + 2.gTerra.dTerra
Marte: v2 = (v0)2 + 2.(-g).Δs => (vMarte)2 = 0 + 2.gMarte.dMarte
Sendo vTerra = vMarte, vem: 2.gTerra.dTerra = 2.gMarte.dMarte => 2.gTerra.dTerra = 2.(gTerra/3).dMarte =>
dMarte = 3.dTerraSendo vTerra = vMarte, vem: 2.gTerra.dTerra = 2.gMarte.dMarte => 2.gTerra.dTerra = 2.(gTerra/3).dMarte =>
Resposta: V,F,V,V









Nenhum comentário:
Postar um comentário