Arte do Blog

Boulevard de Clichy

Paul Signac

Paul Signac nasceu em Paris em 11 de novembro de 1863. O encontro com o Impressionismo, especialmente com o trabalho de Monet, fez com que ele se sentisse induzido a abandonar os estudos de arquitetura e se tornasse pintor.

Calvados

Em 1884 Signac conheceu Georges Seurat e o resultado desta reunião foi a adesão de Signac ao pontilhismo. Depois da morte de Seurat, em 1891, Paul Signac tornou-se o principal porta-voz do movimento Neo-Impressionista, apoiado pelo crítico Félix Fénéon. Em 1899 Signac escreveu uma obra de referência sobre o "Neo-Impressionismo: D'Eugène Delacroix au Néo-Impressionnisme" [De Eugène Delacroix ao Neo-Impressionismo].

Barcos à vela em Les Sables-d Olonne

Em suas pinturas Paul Signac sempre buscou seguir as regras da teoria da cor pontilhista. Signac também fez muitas aquarelas, o que lhe permitiu mais liberdade de expressão. Seus motivos favoritos foram as paisagens do Mediterrâneo, incluindo o mar e os barcos que ele tanto amava.

A sala de jantar

 

Paul Signac não foi apenas importante como um expoente do Neo-Impressionismo. Ele também exerceu uma profunda influência sobre gerações de artistas de sucesso. Foi um dos primeiros a promover Henri Matisse e André Derain, pode-se mesmo afirmar que Signac aplainou o caminho para o fauvismo. 
Sua técnica pontilhista formalmente abstrata também serviu de base para as tendências do século 20, especificamente o cubismo.
Paul Signac morreu em Paris em 15 de agosto de 1935.           

Paris-quai-de-la-tournelle-1886

Saiba mais aqui e aqui

Especial de Sábado

Ganhadores do Premio Nobel de Física

Borges e Nicolau

x

2002 
Raymond Davis Jr. e Masatoshi Koshiba - pelas contribuições pioneiras à astrofísica, em particular pela detecção de neutrinos cósmicos.

Riccardo Giacconi - pelas contribuições pioneiras à astrofísica, que levaram à descoberta das fontes de raios-X cósmicos.

Raymond Davis Jr (1914-2006), físico estadunidense, Masatoshi Koshiba (1926), físico japonês e 
Riccardo Giacconi (1931), físico italiano
 x

Raymond Davis Jr, físico estadunidense e Masatoshi Koshiba, físico japonês dividiram 50% do Premio Nobel de Física em 2002 pelas pioneiras contribuições de ambos à astrofísica, em particular pela descoberta dos neutrinos cósmicos. Davis foi o primeiro cientista a detectar neutrinos formados nos processos de fusão do sol e outras estrelas, quando o hidrogênio se transforma em hélio, revelando como funcionam as estrelas. Para detectar essas partículas, ele colocou em uma mina de ouro um grande tanque de 14,6 metros de comprimento e 6,1 de diâmetro e com 615 toneladas de fluido em seu interior. O físico calculou que, a cada mês, 20 neutrinos reagiriam com os átomos de cloro presentes no fluido, de forma a criar 20 átomos de argônio. Ele desenvolveu um método para extrair e contar esses átomos. Após trinta anos de experimento, iniciado nos anos 1960, detectou 2000 neutrinos solares. Esses resultados foram confirmados pelo grupo de pesquisa de Koshiba, que construiu um outro detector, o Kamiokande, que consistia em um enorme tanque preenchido com água, com a qual alguns neutrinos poderiam interagir.

Riccardo Giacconi foi agraciado com o Prêmio Nobel de Física de 2002, (50%), por suas contribuições à astrofísica, que o conduziram à descoberta de fontes de Raios-X cósmicos. Seus estudos permitiram uma melhor compreensão dos raios-X emitidos pelo Sol e outros astros. Como esse tipo de radiação é invisível e quase totalmente absorvido pela atmosfera da Terra, seu estudo requer o uso de instrumentos enviados para o espaço. A equipe de Giacconi construiu os primeiros telescópios de raios-X e equipou um foguete com equipamentos que detectaram pela primeira vez uma fonte de raios-X fora do Sistema Solar. Sua equipe foi ainda a primeira a provar que o universo contém uma radiação de fundo de raios-X. Eles também detectaram fontes de raios-X que, acredita-se hoje, poderiam conter buracos negros.

Saiba mais aqui

x
Próximo Sábado: Ganhadores do Premio Nobel de 2003: 

Alexei A. Abrikosov, Vitaly L. Ginzburg e Anthony J. Leggett - pelas contribuições pioneiras à teoria dos supercondutores e superfluidos.

Caiu no vestibular

A torneira e as gotas

(UFAM)
Uma torneira pinga em intervalos de tempos iguais. A figura (fora de escala) mostra a situação em que uma das gotas está saindo da torneira. Despreze a resistência do ar e considere que as gotas saem da torneira com velocidade nula. A razão B/A entre as distâncias vale:

a) 9
b) 2
c) 6
d) 12
e) nenhuma das respostas

Resolução: 

Como a torneira pinga em intervalos de tempo iguais, podemos indicar os instantes mostrados na figura, de cima para baixo, como sendo t = 0, T, 2T e 3T.

A = g.T²/2 (1)
B = g.(3T)²/2 => B = 9.g.T²/2 (2)

Dividindo membro a membro (2) por (1), resulta: B/A = 9

Resposta: a

Cursos do Blog - Eletricidade

10ª aula
Propriedades do potencial elétrico

Borges e Nicolau

Uma carga elétrica q>0 é abandonada em repouso em um ponto A de um campo eletrostático, gerado por uma carga elétrica puntiforme Q>0, fixa num ponto O.

Sob ação da força eletrostática a partícula se desloca espontaneamente de A até B. Neste deslocamento a força eletrostática realiza um trabalho positivo (força e deslocamento têm o mesmo sentido, conforme mostra a figura 1. Observe que o potencial elétrico em A é maior do que em B (V_A > V_B).

Se a carga elétrica q fosse negativa ela se deslocaria espontaneamente de A para C e também, neste caso, a força eletrostática teria o sentido do deslocamento e realizaria um trabalho positivo (figura 2).

Observe que o potencial elétrico em A é menor do que em C (V_A < V_C).

Clique para ampliar

Clique para ampliar

Do exposto acima para o campo gerado por uma carga elétrica puntiforme, podemos generalizar e tirar as seguintes propriedades:

1. Cargas elétricas positivas abandonadas em repouso num campo eletrostático e sujeitas apenas à força eletrostática, deslocam-se, espontaneamente, para pontos de menor potencial.

2. Cargas elétricas negativas abandonadas em repouso num campo eletrostático e sujeitas apenas à força eletrostática, deslocam-se, espontaneamente, para pontos de maior potencial.

3. Percorrendo-se uma linha de força no seu sentido o potencial elétrico ao longo de seu pontos diminui.

4. Em todo movimento espontâneo de cargas elétricas num campo eletrostático a energia potencial elétrica diminui e a energia cinética aumenta.

Exercícios básicos

Exercício 1:
Analise as afirmativas e assinale as corretas:

a) Cargas elétricas positivas são abandonadas em repouso em um campo eletrostático e sujeitas apenas à força eletrostática. O trabalho realizado pela força eletrostática é positivo.
b) Cargas elétricas negativas são abandonadas em repouso em um campo eletrostático e sujeitas apenas à força eletrostática. O trabalho realizado pela força eletrostática é negativo.
c) Cargas elétricas positivas abandonadas em repouso em um campo eletrostático e sujeitas apenas à força eletrostática, deslocam-se, espontaneamente, para pontos de maior potencial.
d) Cargas elétricas negativas abandonadas em repouso em um campo eletrostático e sujeitas apenas à força eletrostática, deslocam-se, espontaneamente, para pontos de maior potencial.
e) Observando as linhas de força do campo eletrostático representado abaixo, concluímos que o potencial elétrico no ponto A é menor do que no ponto B.

Resolução:

No deslocamento espontâneo de cargas elétricas em um campo eletrostático, o trabalho da força eletrostática é sempre positivo. Como consequência, cargas elétricas positivas deslocam-se espontaneamente para pontos de menor potencial e cargas negativas para pontos de maior potencial.
Uma propriedade importante a respeito das linhas de força: percorrendo-se uma linha de força no seu sentido o potencial elétrico diminui ao longo de seus pontos.

Nestas condições, são corretas as alternativas: a e d

Resposta: a e d

Exercício 2:
Uma carga elétrica puntiforme é abandonada em repouso em um campo elétrico. Podemos concluir que durante o movimento espontâneo da carga sua energia:

a) cinética aumenta assim como sua energia potencial elétrica
b) potencial elétrica aumenta e sua energia cinética diminui
c) cinética diminui assim como sua energia potencial elétrica
d) potencial elétrica diminui e sua energia cinética aumenta
e) total (cinética + potencial elétrica) diminui.

Resolução:

No deslocamento espontâneo de cargas elétricas abandonadas em um campo elétrico, a energia potencial elétrica diminui e consequentemente a energia cinética aumenta de modo que a energia mecânica (soma das energias potencial e cinética) permanece constante.

Resposta: d 

Exercício 3:
Uma partícula eletrizada com carga q = -2 µC é transportada por um operador de um ponto A, cujo potencial é V_A = 3.10³ V,  até um ponto B cujo potencial 
é V_B = 1.10³ V. A partícula parte com velocidade nula do ponto A e chega ao ponto B com velocidade também nula.

a) Qual é o trabalho da força elétrica que age na partícula no deslocamento de A até B?
b) Qual é o trabalho da força que o operador aplica na partícula no deslocamento de A até B?

Resolução:

a) τ_AB = q.(V_A-V_B) = -2.10^-6.(3.10³-1.10³) => τ_AB = -4.10^-3 J

b) Teorema da energia cinética:

τ_operador + τ_{força elétrica} = E_cin(final) - E_cin(inicial) =>
τ_operador + (-4.10³) = 0 - 0 => 
τ_operador = 4.10³ J

Respostas: a) -4.10^-3 J; b) 4.10³ J

Exercício 4:
Uma partícula eletrizada percorre uma linha de força de um campo eletrostático passando pelos pontos A, B e C. A partícula desloca-se sob ação da força eletrostática somente. Sejam E_c a energia cinética da partícula, E_P sua energia potencial elétrica e E_M sua energia mecânica (soma das energias cinética e potencial). Preencha a tabela abaixo:

Clique para ampliar

Resolução:

Conhecendo-se, na posição A, as energias potencial (0,3 J) e cinética (0,5 J), concluímos que a energia mecânica é igual a 0,8 J. Esta energia permanece constante. Assim podemos preencher a tabela dada:

Resposta: ver tabela acima 
 

Exercício 5:
Retome o exercício anterior. Determine o trabalho da força eletrostática que age na partícula nos deslocamentos de:

a) A para B;
b) A para C.

Resolução:

a)
τ_AB = q.(V_A-V_B) = q.V_A - q.V_B => τ_AB = E_pA - E_pB =>
τ_AB = 0,3 J - 0,2 J = 0,1 J
b)
τ_AC = E_pA - E_pC = 0,3 J - 0,1 J = 0,2 J

x

Respostas: a) 0,1 J; b) 0,2 J
 

Exercícios de revisão

Revisão/Ex 1:
(UNIP-SP)
Um ponto material eletrizado é colocado em repouso sob ação exclusiva de um campo eletrostático uniforme. Podemos afirmar que o ponto material vai deslocar-se:

a) de modo a diminuir sua energia potencial elétrica;
b) de modo a diminuir o potencial elétrico;
c) no mesmo sentido da linha de força do campo;
d) em movimento retilíneo e uniforme;
e) de modo a aumentar sua energia mecânica.

Resolução:

O movimento do ponto material no campo eletrostático é espontâneo. Nestas condições, a energia potencial elétrica diminui, a energia cinética aumenta e a energia mecânica é constante.
A partícula pode ou não se deslocar no sentido da linha de força dependendo do sinal da carga elétrica. A força eletrostática que age na partícula é constante, pois o campo é uniforme. Logo o movimento da partícula é um MUV.

Resposta: a

Revisão/Ex 2:
(FCMSC-SP)
Quando forem aproximadas duas partículas que se repelem, a energia potencial elétrica das duas partículas;

a) aumenta
b) diminui
c) fica constante
d) diminui e em seguida aumenta
e) aumenta e em seguida diminui

Resolução:

Se as partículas se repelem, concluímos que elas estão eletrizadas com cargas elétricas de mesmo sinal. Para serem aproximadas o operador despende energia que fica armazenada no sistema de cargas sob a forma de energia potencial. Isto significa que a energia potencial das duas partículas aumenta. Observe que a aproximação, neste caso, não é um movimento espontâneo.

Resposta: a

Revisão/Ex 3:
(PUC-SP) 
Assinale a afirmação falsa :

a) Uma carga negativa abandonada em repouso num campo eletrostático fica sujeita uma força que realiza sobre ela um trabalho negativo.

b) Uma carga positiva abandonada em repouso num campo eletrostático fica sujeita uma força que realiza sobre ela um trabalho positivo.

c) Cargas negativas abandonadas em repouso num campo eletrostático dirigem-se para pontos de potencial mais elevado.

d) Cargas positivas abandonadas em repouso num campo eletrostático dirigem-se para pontos de menor potencial.

e) O trabalho realizado pelas forças eletrostáticas ao longo de uma curva fechada é nulo.

Resolução:

Uma carga elétrica negativa, abandonada em repouso em um ponto de um campo eletrostático, fica sob ação de uma força eletrostática e se desloca espontaneamente. Neste deslocamento a força eletrostática realiza um trabalho positivo, pois ela e o deslocamento têm mesmo sentido.
Portanto, a alternativa a) é falsa.

Resposta: a 

Este enunciado refere-se aos testes 4 e 5.
A figura mostra um conjunto de linhas de força de um campo elétrico, obtidas ao mapear o campo produzido por uma determinada distribuição de cargas.

Revisão/Ex 4:
Considerando as superfícies equipotenciais V₁, V₂ e V₃, podemos airmar que:

a) V₁ > V₂ 
b) V₃ > V₁ 
c) V₂ < V₃ 
d) V₂ > V₁ 
e) nenhuma das anteriores

Resolução:

Vimos que percorrendo-se uma linha de força no seu sentido o potencial elétrico ao longo de seu pontos diminui. Portanto, concluímos que: V₁ > V₂ > V₃.

Resposta: a

Revisão/Ex 5:
Com relação às intensidades dos campos elétricos nos pontos A, B e C, podemos afirmar que:

a) E_A < E_B
b) E_A > E_C
c) E_A = E_B = E_C 
d) E_B < E_A 
e) nenhuma das anteriores

Resolução:

Vimos que na região onde as linhas de força estão mais próximas a intensidade do vetor campo elétrico é maior. Assim, E_C > E_B > E_A.

Resposta: a

Cursos do Blog - Termologia, Óptica e Ondas

10ª aula
Mudanças de fase (III)

Borges e Nicolau

Influência da pressão nas temperaturas de fusão e de ebulição

A maioria das substâncias aumenta de volume na fusão e, portanto, diminui de volume ao se solidificar. Para estas substâncias, um aumento de pressão acarreta um aumento na temperatura de fusão.

Clique para ampliar

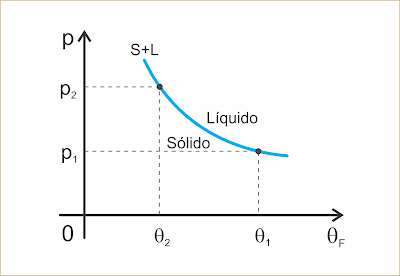
Existem exceções, como por exemplo a água. Para estas substâncias o volume diminui na fusão e, portanto, aumenta na solidificação. Para as exceções, um aumento de pressão acarreta uma diminuição na temperatura de fusão.

Clique para ampliar

Para todas as substâncias, um aumento de pressão acarreta um aumento na temperatura de ebulição.

Clique para ampliar

Diagrama de fases

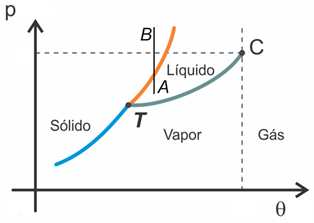
Maioria das substâncias (como por exemplo o CO₂)

Clique para ampliar

Exceções (como por exemplo a água)

Clique para ampliar

Curva de fusão (1)

Delimita as regiões correspondentes às fases sólida e líquida. Cada ponto dela é representativo de um estado de equilíbrio entre essas fases.

Curva de vaporização (2)

Delimita as regiões correspondentes às fases líquida e de vapor. Cada ponto dela é representativo de um estado de equilíbrio entre essas fases.

Curva de sublimação (3)

Delimita as regiões correspondentes às fases sólida e de vapor. Cada ponto dela é representativo de um estado de equilíbrio entre essas fases.

Ponto triplo ou tríplice (T)

Estado comum às três curvas; é representativo do equilíbrio entre as três fases da substância.

Ponto crítico (C)

Estado em que corresponde à mais alta temperatura em que a substância é um vapor.

Vapor (θ ≤ θ_c): liquefaz-se por compressão isotémica.

Gás (θ > θ_c): não se liquefaz por compressão isotérmica.

Clique para ampliar

Animação:
Diagrama de fases
Clique aqui

Exercícios básicos

Exercício 1:

Uma determinada porção de uma substância passa do estado líquido para o estado sólido. A porção de sólido obtida flutua sobre a parte que ainda está líquida. Pode-se afirmar que:

a) O volume da substância diminui com a solidificação.

b) Os estados sólido e líquido desta substância têm mesma densidade.

c) Para esta substância um aumento de pressão acarreta uma diminuição na temperatura de fusão.

d) Para esta substância um aumento de pressão acarreta um aumento na temperatura de fusão.

e) A temperatura de fusão desta substância é a mesma, qualquer que seja a pressão sobre ela exercida.

Resolução:

Se a porção sólida flutua no líquido, concluímos que a densidade da substância no estado sólido é menor do que no estado líquido. Logo, esta substância ao se solidificar aumenta de volume. Ela pertence às exceções. Portanto, para ela um aumento de pressão acarreta uma diminuição na temperatura de fusão.

Resposta: c

x

Exercício 2:

Um aumento da pressão sobre o gelo faz com que sua temperatura de fusão:

a) mantenha-se constante

b) diminua
c) aumente
d) aumente e a seguir diminua
e) diminua e a seguir aumente

Resolução:

A água é uma exceção. Um aumento de pressão sobre o gelo acarreta uma diminuição na temperatura de fusão.

Resposta: b
x
Exercício 3:
Você sabe que a água entra em ebulição a 100 ºC quando sob pressão normal (1 atm). É possível ferver a água à temperatura ambiente?

Resolução:

Sim, desde que a pressão sobre a água seja bem menor do que 1 atm. 

Exercício 4:
Analise a proposição abaixo e assinale se está certa ou errada.

"O ponto de ebulição da água é sempre 100 ºC em qualquer ponto da superfície terrestre, mesmo que ela esteja sendo fervida em recipientes abertos e em locais de altitudes diferentes".

Resolução:

Com o aumento da altitude diminui a pressão sobre a água e menor é a temperatura de ebulição.
x
Exercício 5:
Analise a proposição abaixo e assinale se está certa ou errada.

"Quando a água é aquecida numa panela de pressão fechada, a temperatura atingida é maior do que 100 ºC pois a pressão no interior da panela é maior do que 1 atm".

Resolução:

Certa. Quanto maior a pressão maior é a temperatura de ebulição.
x
Exercício 6:
O diagrama de fases apresentado abaixo é de uma substância hipotética.

Clique para ampliar

a) Em que fase a substância se encontra quando sob pressão de 300 mm Hg e à temperatura de 10 ºC?
b) Em que fase a substância se encontra quando sob pressão de 300 mm Hg e à temperatura de 30 ºC?
c) Qual é o nome da mudança de fase que ocorre quando a substância passa de B para A?
d) Qual é o nome da mudança de fase que ocorre quando a substância passa de D para E?
e) Em que fase a substância não poderá se encontrar se estiver submetida a uma pressão inferior à do ponto triplo T?
f) Sendo C o ponto crítico, é possível liquefazer a substância, por meio de uma compressão isotérmica, estando à temperatura de 70 ºC?

Resolução:

a) Sólida: corresponde ao ponto A do diagrama
b) Líquida: corresponde ao ponto B do diagrama
c) Solidificação: a substância passa do estado líquido para o estado sólido.
d) Liquefação ou Condensação: a substância passa do estado gasoso para o estado líquido
e) A substância não poderá estar na fase Liquida
f) Para θ > θ_c, a substância (gás) não se liquefaz por compressão isotérmica.

Respostas:
a) Sólida
b) Líquida
c) Solidificação
d) Liquefação ou Condensação
e) Liquida
f) Não é possível liquefazer 

Exercícios de revisão

Revisão/Ex 1:
(Fatec–SP)
Uma porção de certa substância está passando do estado líquido para o estado sólido. Verifica-se que o sólido que se forma flutua sobre a parte ainda líquida. Com essa observação, é correto concluir que:

a) a densidade da substância aumenta com a solidificação
b) a massa da substância aumenta com a solidificação
c) a massa da substância aumenta com a fusão
d) o volume da substância aumenta com a fusão
e) o volume da substância aumenta com a solidificação

Resolução:

Se o sólido que se forma flutua sobre a parte ainda líquida, concluímos que a densidade do sólido é menor do que a do líquido. Logo, o volume da substância aumenta na solidificação.

Resposta: e

Revisão/Ex 2:
(Unifor–CE)
Acerca das mudanças de fase das substâncias, considere as afirmativas que seguem.
I. Se uma substância aumenta de volume ao sofrer fusão, um aumento de pressão sobre ela deverá diminuir o seu ponto de fusão.
II. Um líquido pode se solidificar, à temperatura constante, apenas por elevação da pressão sobre ele.
III. Uma substância, mantida à temperatura constante e menor que a do ponto tríplice, pode passar do estado sólido ao gasoso apenas por redução da pressão.
Dentre essas afirmativas, somente:

a) I é correta.                    b) II é correta.                     c) III é correta.
d) I e II são corretas.          e) II e III são corretas.

Resolução:

I. Incorreta. Se a substância aumenta de volume ao sofrer fusão ela pertence à maioria das substâncias. Portanto, um aumento de pressão sobre ela deverá aumentar o seu ponto de fusão.
 
II. Correta. Um líquido pode se solidificar à temperatura constante apenas por elevação da pressão sobre ele, conforme se observa no diagrama abaixo (A→B):

                 
III. Correta. Uma substância, mantida à temperatura constante e menor que a do ponto tríplice, pode passar do estado sólido ao gasoso apenas por redução da pressão, conforme se observa no diagrama abaixo (A→B):

Resposta: e

Revisão/Ex 3:
(VUNESP)
A liofilização é um processo de desidratação de alimentos que, além de evitar que seus nutrientes saiam junto com a água, diminui bastante sua massa e seu volume, facilitando o armazenamento e o transporte. Alimentos liofilizados também têm seus prazos de validade aumentados, sem perder características como aroma e sabor.

O processo de liofilização segue as seguintes etapas:
I. O alimento é resfriado até temperaturas abaixo e 0 °C para que a água contida nele seja solidificada.
II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada.
Dessa forma, a água sai do alimento sem romper suas estruturas moleculares, evitando perdas de proteínas e vitaminas.
O gráfico mostra parte do diagrama de fases da água e cinco processos de mudança de fase, representados pelas setas numeradas de 1 a 5.

A alternativa que melhor representa as etapas do processo de liofilização, na ordem descrita, é:

a) 4 e 1.               b) 2 e 1.               c) 2 e 3.
d) 1 e 3.               e) 5 e 3.

Resolução:

I. Ao se resfriar o alimento até temperaturas abaixo de 0 °C, a água nele contida se solidifica. Assim, tem-se a passagem do estado líquido para o sólido, o que é representado pela seta 2.

II. A sublimação, passagem direta do estado sólido para o estado gasoso, é representada pela seta 3.

Resposta: c

Revisão/Ex 4:
(UDESC-SC)
Para cada substância simples pode-se fazer um gráfico, denominado diagrama de fase, em que cada ponto corresponde a uma combinação de pressão e temperatura bem definidas. Essa combinação de pressão e temperatura determina a fase da substância. A figura mostra o diagrama de fase da água.

Analisando o diagrama de fase da água, todas as alternativas estão corretas, exceto a:

a) O ponto A é o ponto triplo da água.
b) A água está na fase gasosa no ponto Z.
c) A curva AB é a curva de vaporização.
d) A água está na fase sólida no ponto X.
e) O ponto B é o ponto de ebulição da água nas condições normais de temperatura (0 °C) e pressão (1 atm).

Resolução:

No estado representado pelo ponto Z a água está na fase líquida. 

Resposta: b

Revisão/Ex 5:
(FMABC-SP)
O gráfico representa o diagrama de fases do “gelo seco”. PT e PC representam, respectivamente, ponto triplo e ponto crítico da substância.

Analise este diagrama e assinale a alternativa correta.

a) Acima de 31 ºC, a substância apresenta-se no estado gasoso.
b) É possível liquefazer o gás apenas aumentando a temperatura de - 56,6 ºC para 31 ºC.
c) A substância apresenta-se no estado sólido para valores de pressão acima de uma atmosfera.
d) A substância apresenta-se sempre no estado líquido para a temperatura de 20 ºC.
e) A substância apresenta-se em mudança de estado para a pressão de 5,1 atm e temperatura de -10 ºC.

Resolução:

A temperatura de 31 °C corresponde à temperatura crítica do CO₂. Acima desta temperatura a substância é um gás.

Resposta: a