Cinemática vetorial (III)
Borges e Nicolau
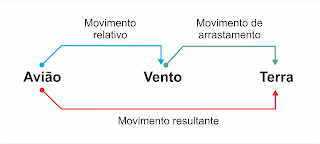
Composição de movimentos
Considere um barquinho movendo-se nas águas de um rio. O movimento do barquinho em relação às águas chama-se movimento relativo.
O movimento das águas que arrastam o barquinho em relação às margens é o movimento de arrastamento.
O movimento do barquinho em relação às margens, isto é, em relação à Terra, é o movimento resultante.
A velocidade do barquinho em relação às águas é a velocidade relativa
(vrel).
A velocidade das águas, isto é, a velocidade da correnteza é a velocidade de arrastamento (varr).
A velocidade do barquinho em relação às margens é a velocidade resultante (vres).
Tem-se a relação vetorial:
Portanto: a velocidade do movimento resultante é a soma vetorial das velocidades dos movimentos relativo e de arrastamento.
Considere os casos:
Clique para ampliar
Clique para ampliar
Clique para ampliar
Clique para ampliar
Exercícios básicos
Exercício 1:
Um barco desce um rio com velocidade em relação às margens de módulo 20 m/s e, a seguir, sobe o rio com velocidade de 8,0 m/s também em relação às margens. Determine o módulo da velocidade do barco em relação às águas, considerado o mesmo na subida e na descida e o módulo da velocidade da correnteza.
Resolução:
Vamos indicar por vres, vrel e varr os módulos das velocidades resultante, relativa e de arrastamento. Podemos escrever:
Barco descendo o rio: vres = vrel + varr => 20 = vrel + varr (1)
Barco subindo o rio: vres = vrel - varr => 8,0 = vrel - varr (2)
De (1) e (2):
vrel = 14 m/s e varr = 6,0 m/s
Respostas: 14 m/s e 6,0 m/s
Exercício 2:
Um ônibus se desloca em movimento retilíneo e uniforme com velocidade de módulo 72 km/h, em relação a uma estrada.
Um menino sai da parte traseira do ônibus e com passadas regulares se desloca até à parte dianteira, percorrendo em 5 s a distância de 10 m em relação ao ônibus. Determine:
a) O módulo da velocidade do menino em relação ao ônibus e em relação à estrada.
b) A distância que o menino percorre, em relação à estrada ao se deslocar da parte traseira até à parte dianteira do ônibus.
Sugestão:
Clique para ampliar
Resolução:
a) vrel = Δsrel/Δt = 10 m/5 s => vrel = 2m/s = 7,2 km/h
vres = vrel + varr => vres = 2 + 20 => vres = 22 m/s = 79,2 km/h
b) vres = Δsrel/Δt => 22 = Δsrel/5 => Δsrel = 110 m
Respostas:
a) 2m/s = 7,2 km/h e 22 m/s = 79,2 km/h;
b) 110 m
Exercício 3:
Um barco atravessa um rio de margens paralelas e de largura 2,0 km, com velocidade em relação à correnteza de módulo 8,0 km/h. O barco sai de um ponto A de uma margem e mantém seu eixo sempre perpendicular à correnteza, atingindo a outra margem.
A velocidade da correnteza é constante e de módulo igual a 6,0 km/h. Determine:
a) o módulo da velocidade resultante do barco;
b) a duração da travessia;
c) o módulo da velocidade resultante do barco para que ele saia de A e atinja um ponto B da margem oposta, exatamente em frente ao ponto A de partida.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (8,0)2 + (6,0)2 => vres = 10 km/h
b) vrel = Δsrel/Δt => 8,0 = 2,0/Δt => Δt = (1/4) h = 15 min
c) (vrel)2 = (vres)2 + (varr)2 => (8,0)2 = (vres)2 + (6,0)2 =>
vres = √28 km/h ≅ 5,3 km/h
Respostas: a) 10 km/h; b) 15 min c) √28 km/h => ≅ 5,3 km/h
Exercício 4:
Um avião possui em relação à Terra uma velocidade de 600 km/h, na direção norte-sul e sentido de sul para norte. Repentinamente o avião enfrenta um forte vento com velocidade, em relação à Terra, de 100 km/h, na direção oeste-leste e no sentido de oeste para leste. Para que o avião continue em sua rota original, qual deve ser o módulo da velocidade do avião em relação ao ar e qual é aproximadamente o ângulo que o eixo longitudinal do avião deve fazer com a direção norte-sul? É dada a tabela:
Clique para ampliar
Sugestão:
Clique para ampliar
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (600)2 + (100)2 =>
vrel = √37.102 km/h ≅ 608,3 km/h
tg θ = varr/vrel = 100/608,3 ≅ 0,17 => θ ≅ 10º
Respostas: √37.102 km/h => 608,3 km/h; aproximadamente 10º
Exercício 5:
A chuva cai verticalmente com velocidade de módulo 3,0 m/s, em relação ao solo. Não há ventos. Uma pessoa caminha horizontalmente com velocidade de módulo √3 m/s. Para não se molhar ela inclina seu guarda-chuva de um ângulo θ com a horizontal. Qual é o valor de θ?
Clique para ampliar
Sugestão:
Clique para ampliar
Resolução:
tg θ = vres/varr = 3/√3 = √3 => θ = 60º
Resposta: 60º
Revisão/Ex 1:
(U. Mackenzie-SP)
Uma lancha, subindo um rio, percorre em relação às margens, 2,34 km em 1 h 18 min. Ao descer o rio, percorre a mesma distância em 26 min. Observa-se que, tanto na subida como na descida, o módulo da velocidade da lancha em relação á água é o mesmo. O módulo da velocidade da correnteza em relação às margens é:
a) 5,4 km/h b) 4,5 km/h c) 3,6 km/h d) 2,7 km/h e) 1,8 km/h
Resolução:
Barco subindo o rio:
vres = vrel - varr => 2,34km/1,3h = vrel - varr => 1,8 km/h = vrel - varr (1)
Barco descendo o rio:
vres = vrel + varr => 2,34km/(26/60)h = vrel + varr => 5,4 km/h = vrel + varr (2)
De (1) e (2):
vrel = 3,6 km/h e varr = 1,8 km/h (velocidade da correnteza)
Resposta: e
Revisão/Ex 2:
(ITA-SP)
Um barco, com motor em regime constante, desce um trecho retilíneo de um rio em 2,0 h e sobe o mesmo trecho em 4,0 h. Quanto tempo levará o barco para percorrer o mesmo trecho, rio abaixo, com o motor desligado? Admita que a velocidade da correnteza seja constante.
a) 3,0 h b) 4,0 h c) 6,0 h d) 8,0 h e) 10 h
Resolução:
Barco desce o rio: vres = vrel + varr => d/2,0 = vrel + varrr (1)
Barco sobe o rio: vres = vrel - varr => d/4,0 = vrel - varrr (2)
(1) – (2): d/4,0 = 2.varr (3)
Para percorrer o mesmo trecho, rio abaixo, com o motor desligado, a velocidade do barco é a mesma da correnteza, isto é, de arrastamento.
Assim, de (3), vem:
d/4,0 = 2.(d/Δt ) => Δt = 8,0 h
Resposta: d
Revisão/Ex 3:
(UFMT)
Uma pessoa tem velocidade, relativa a uma esteira, de módulo 1,5 m/s e direção perpendicular à da velocidade de arrastamento da esteira. A largura da esteira é de 30 m e sua velocidade de arrastamento, em relação ao solo, tem módulo igual a 2,0 m/s. Calcule:
a) o módulo da velocidade da pessoa em relação ao solo.
b) a distância percorrida pela pessoa, em relação ao solo, ao atravessar a esteira.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (1,5)2 + (2,0)2 => vres = 2,5 m/s
b) vrel = AB/Δt => 1,5 = 30/Δt => Δt = 20 s
vres = AC/Δt => 2,5 = AC/20 => AC = 50 m
Respostas: a) 2,5 m/s b) 50 m
Revisão/Ex 4:
(EFEI-MG)
Um barco atravessa um rio seguindo a menor distância entre as margens que são paralelas. Sabendo que a largura do rio é de 2,0 km, que a travessia é feita em 15 min e que a velocidade da correnteza é 6,0 km/h, podemos afirmar que a velocidade do barco em relação à água é:
a) 2,0 km/h
b) 6,0 km/h
c) 8,0 km/h
d) 10 km/h
e) 14 km/h
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (2,0km/0,25h)2 + (6,0)2 => vrel = 10 km/h
Resposta: d
Revisão/Ex 5:
(Fatec-SP)
Sob chuva que cai verticalmente, uma pessoa caminha horizontalmente com velocidade 1,0 m/s, inclinando o guarda-chuva a 30º (em relação à vertical), para resguardar-se o melhor possível. Dado que tg 60º = 1,7, a velocidade da chuva em relação ao solo:
a) é 1,7 m/s
b) é 2,0 m/s
c) é 0,87 m/s
d) depende do vento.
e) depende da altura da nuvem de origem.
Resolução:
tg 60° = vres/varr => 1,7 = vres/1,0 => vres = 1,7 m/s
Resposta: a
Resposta: a












Nenhum comentário:
Postar um comentário