Lembrete: O primeiro seguidor do Blog que enviar a resolução correta deste exercício receberá um livro como premio. Mãos à obra pois...
Bloco descendo sem atrito
Um bloco B1 parte do repouso do topo (A) de outro bloco B2, cuja face superior é um plano inclinado. Não há atrito entre2todas as superfícies em contato. As massas de B1 e B2 são, respectivamente, m e 3m.
Sendo H = 4,2 m, g = 10 m/s2, sen θ = 0,6 e cos θ = 0,8, a velocidade2que o bloco B2 adquire, no instante em que o bloco B1 atinge o ponto B é igual a:
a) 1 m/s b) 2 m/s c) 3 m/s d) 4 m/s e) 5 m/s
sexta-feira, 31 de maio de 2013
quinta-feira, 30 de maio de 2013
Caiu no vestibular
Girando sem deslizar
(Fuvest-SP)
Um disco roda sobre uma superfície plana, sem deslizar. A velocidade do centro O é v0. Em relação ao plano:
a) qual é a velocidade vA do ponto A?
b) qual é a velocidade vB do ponto B?
Resolução:
Vamos resolver este exercício por composição de dois movimentos: um de translação e outro de rotação em torno do centro O. No movimento de translação todos os pontos se deslocam com velocidade de módulo v0. No movimento de rotação, em torno do centro O, todos os pontos da circunferência giram com velocidade de módulo v0. Para o movimento resultante, temos: vB = 2.v0 e vA = 0.
Observe que a velocidade do ponto A é nula, pois o disco roda sem deslizar.
Respostas:
a) vB = 2.v0
b) vA = 0
(Fuvest-SP)
Um disco roda sobre uma superfície plana, sem deslizar. A velocidade do centro O é v0. Em relação ao plano:
a) qual é a velocidade vA do ponto A?
b) qual é a velocidade vB do ponto B?
Resolução:
Vamos resolver este exercício por composição de dois movimentos: um de translação e outro de rotação em torno do centro O. No movimento de translação todos os pontos se deslocam com velocidade de módulo v0. No movimento de rotação, em torno do centro O, todos os pontos da circunferência giram com velocidade de módulo v0. Para o movimento resultante, temos: vB = 2.v0 e vA = 0.
Observe que a velocidade do ponto A é nula, pois o disco roda sem deslizar.
Respostas:
a) vB = 2.v0
b) vA = 0
terça-feira, 28 de maio de 2013
Cursos do Blog - Termologia, Óptica e Ondas
15ª aula
Estudo dos gases (III)
Borges e Nicolau
Teoria Cinética dos Gases
No estudo do comportamento de um gás, consideramos o seguinte modelo:
• as moléculas do gás movimentam-se caoticamente;
• os choques entre as moléculas e contra as paredes do recipiente são perfeitamente elásticos;
• as moléculas não exercem forças entre si, exceto quando colidem;
• as moléculas apresentam volume próprio desprezível em comparação com o volume ocupado pelo gás.
O gás que obedece a este modelo é chamado gás perfeito ou gás ideal. Um gás real submetido a altas temperaturas e baixas pressões apresenta um comportamento que se aproxima ao de um gás ideal.
A pressão p exercida por um gás perfeito pode ser dada em função da densidade μ do gás e da velocidade média v de suas moléculas:
De p = (1/3).μ.v2, vem:
A energia cinética de um determinado número de mols de um gás perfeito é diretamente proporcional à temperatura absoluta.
De Ec = (3/2).n.R.T, resulta:
A velocidade média das moléculas de um gás perfeito, a uma certa temperatura, depende da natureza do gás, dada pela massa molar M.
Seja N o número de moléculas do gás. A energia cinética média por molécula é dada por:
Sendo NA o número de Avogadro, podemos calcular o número de mols, dividindo N por NA: n = N/NA . Assim, temos:
A relação R/NA = k é denominada constante de Boltzmann e é igual a
1,38.10-23 J/K. Portanto:
Gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula.
Exercícios básicos
Exercício 1:
Um gás perfeito sofre uma transformação isobárica e seu volume é reduzido à metade do valor inicial. A temperatura absoluta do gás:
a) permanece a mesma;
b) duplica
c) triplica
d) cai à metade
e) fica três vezes menor
Resolução:
Sendo a transformação isobárica, temos: V/T = constante. Se o volume V é reduzido à metade, a temperatura absoluta T também cai à metade.
Resposta: d
Exercício 2:
O que ocorre com a energia cinética do gás em virtude da transformação descrita na questão 1?
a) permanece a mesma;
b) duplica
c) quadruplica
d) cai à metade
e) fica quatro vezes menor
Resolução:
De Ec = 3.n.R.T/2 concluímos que reduzindo-se T à metade, o valor de Ec também cai à metade.
Resposta: d
Exercício 3:
Certa massa de um gás perfeito sofre uma transformação de modo que sua temperatura aumenta de 127 ºC para 327 ºC. A relação entre as energias cinéticas do gás entre os estados inicial e final é igual a:
a) 1/3 b) 2/3 c) 1 d) 4/3 e) 5/3
Resolução:
127 ºC => T1 = 400 K e 327º C => T2 = 600 KEc1/Ec2 = T1/T2 = 400/600 = 2/3
Resposta: b
Exercício 4:
Um mol de um gás perfeito ocupa o volume de 22,4 L, sob pressão de
1 atm e a 0 ºC. Sendo 1 atm = 105 N/m2 e 1 L = 10-3 m3, qual é a energia cinética do gás?
Resolução:
Ec = 3.n.R.T/2 => Ec = 3.p.V/2 = 3.105.22,4.10-3/2 => Ec = 3,36.103 J
Resposta: 3,36.103 J
Exercício 5:
Considere um recipiente contendo um gás perfeito. Analise as afirmações:
I) A energia cinética do gás independe da temperatura a que o gás se encontra.
II) A 0 ºC a energia cinética do gás é nula.
III) A energia cinética média por molécula independe da natureza do gás.
Tem-se:
a) Somente a afirmação I) é correta.
b) Somente a afirmação II) é correta.
c) Somente a afirmação III) é correta.
d) Todas as afirmações são corretas.
e) Somente duas das afirmações são corretas.
Resolução:
I) Incorreta. A energia cinética de um determinado número de mols de um gás é diretamente proporcional à temperatura absoluta.
II) Incorreta. 0º C corresponde a T = 273 K
III) Correta. A energia cinética média por molécula (ec = 3.k.T, onde k é a constante de Boltzmann) independe da natureza do gás: Gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula.
x
Resposta: c
x
Exercício 6:
Dois recipientes, A e B, contém gases de naturezas diferentes. Os gases estão à mesma temperatura. O gás do recipiente A tem massa molar maior do que a do recipiente B. Sejam vA e vB as velocidades médias das moléculas de A e B, respectivamente. Pode-se afirmar que:
a) vA = vB
b) vA > vB
c) vA < vB
d) vA = 2vB
e) vA = vB/2
Resolução:
De v2 = 3.R.T/M, sendo MA > MB, resulta que: vA < vB
Resposta: c
Exercícios de revisão
Revisão/Ex 1:
(ACAFE-SC)
Considerando p a pressão, V o volume e N o número de moléculas de um certo gás ideal, a energia cinética média por molécula desse gás pode ser escrita:
a) Np/2V b) 2pV/3N c) 3pN/2V d) 2pN/3V e) 3pV/2N
Resolução:
A energia cinética de um gás ideal é dada por Ec = 3.p.V/2.
Sendo N o número de moléculas, concluímos que a energia cinética média por molécula é ec = 3.p.V/2N
Resposta: e
Revisão/Ex 2:
(UFRN)
Um gás ideal contido num recipiente sofre uma mudança de temperatura de 300 K para 1.200 K. Qual a razão entre as velocidades médias das moléculas desse gás (v300/v1200)?
Resolução:
De v2 = 3.R.T/M e sendo T1 = 300 K e T2 = 1200 K, vem: (v300/v1200)2 = T1/T2 => (v300/v1200)2 = 300/1200 => v300/v1200 = 1/2
Resposta: 1/4
Revisão/Ex 3:
(UPE)
Em relação à teoria cinética molecular dos gases, é CORRETO afirmar que:
a) a energia cinética média de um conjunto de moléculas de um gás depende, apenas e exclusivamente, das massas das moléculas desse gás.
b) quando quadruplicamos a temperatura absoluta de um conjunto de moléculas de um gás, suas moléculas terão velocidade média quadruplicada.
c) quanto maiores as interações entre as moléculas de um gás, mais rigorosamente ele se comportará como um gás ideal.
d) numa mesma temperatura, independentemente das massas molares de cada gás, as moléculas têm energias cinéticas médias iguais.
e) as colisões entre moléculas de um gás perfeito com as paredes do recipiente que as contém são inelásticas para qualquer tipo de gás ideal.
Resolução:
A energia cinética média por molécula é dada por ec = 3.k.T/2, onde k é a constante de Boltzmann. Observe que gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula. Portanto, a alternativa d é a correta.
Resposta: d
Revisão/Ex 4:
(UNIFEI)
De acordo com a teoria cinética dos gases, a energia cinética média das moléculas que constituem um gás é proporcional à temperatura desse gás. Considere um gás à temperatura ambiente (27 ºC), constituído por moléculas de hidrogênio e de oxigênio. Sabendo que as massas atômicas do hidrogênio e do oxigênio são iguais a 1,0 u.m.a. e 16,0 u.m.a., respectivamente, quais moléculas se movem com maiores velocidades: as moléculas de hidrogênio ou as de oxigênio? Justifique.
Resolução:
De v2 = 3.R.T/M, para o mesmo T e Mhidrogênio < Moxigênio, concluímos que as moléculas de hidrogênio se movem com maiores velocidades.
Revisão/Ex 5:
(UFU-MG)
Considere uma amostra de hidrogênio e outra de oxigênio, ambas a uma mesma temperatura. Sabe-se que a massa molecular do hidrogênio é 3,3.10-27 kg e a do oxigênio é 53.10-27 kg. Podemos afirmar que:
a) Se duplicarmos a temperatura absoluta das amostras , os valores das energias cinéticas médias das moléculas não se alteram.
b) A energia cinética das moléculas de hidrogênio é menor que a energia cinética das moléculas de oxigênio.
c) A velocidade média das moléculas de oxigênio é maior que a velocidade média das moléculas de hidrogênio.
d) A energia cinética das moléculas de hidrogênio não se anula no zero absoluto.
e) A energia cinética das moléculas de oxigênio se anula no zero absoluto.
Resolução:
Estudo dos gases (III)
Borges e Nicolau
Teoria Cinética dos Gases
Gás ideal ou gás perfeito
No estudo do comportamento de um gás, consideramos o seguinte modelo:
• as moléculas do gás movimentam-se caoticamente;
• os choques entre as moléculas e contra as paredes do recipiente são perfeitamente elásticos;
• as moléculas não exercem forças entre si, exceto quando colidem;
• as moléculas apresentam volume próprio desprezível em comparação com o volume ocupado pelo gás.
O gás que obedece a este modelo é chamado gás perfeito ou gás ideal. Um gás real submetido a altas temperaturas e baixas pressões apresenta um comportamento que se aproxima ao de um gás ideal.
Pressão p exercida por um gás perfeito
A pressão p exercida por um gás perfeito pode ser dada em função da densidade μ do gás e da velocidade média v de suas moléculas:
Energia Cinética do gás perfeito
De p = (1/3).μ.v2, vem:
A energia cinética de um determinado número de mols de um gás perfeito é diretamente proporcional à temperatura absoluta.
Velocidade média das moléculas do gás
De Ec = (3/2).n.R.T, resulta:
A velocidade média das moléculas de um gás perfeito, a uma certa temperatura, depende da natureza do gás, dada pela massa molar M.
Energia Cinética média por molécula do gás
Seja N o número de moléculas do gás. A energia cinética média por molécula é dada por:
Sendo NA o número de Avogadro, podemos calcular o número de mols, dividindo N por NA: n = N/NA . Assim, temos:
A relação R/NA = k é denominada constante de Boltzmann e é igual a
1,38.10-23 J/K. Portanto:
Gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula.
Exercícios básicos
Exercício 1:
Um gás perfeito sofre uma transformação isobárica e seu volume é reduzido à metade do valor inicial. A temperatura absoluta do gás:
a) permanece a mesma;
b) duplica
c) triplica
d) cai à metade
e) fica três vezes menor
Resolução:
Sendo a transformação isobárica, temos: V/T = constante. Se o volume V é reduzido à metade, a temperatura absoluta T também cai à metade.
Resposta: d
Exercício 2:
O que ocorre com a energia cinética do gás em virtude da transformação descrita na questão 1?
a) permanece a mesma;
b) duplica
c) quadruplica
d) cai à metade
e) fica quatro vezes menor
Resolução:
De Ec = 3.n.R.T/2 concluímos que reduzindo-se T à metade, o valor de Ec também cai à metade.
Resposta: d
Exercício 3:
Certa massa de um gás perfeito sofre uma transformação de modo que sua temperatura aumenta de 127 ºC para 327 ºC. A relação entre as energias cinéticas do gás entre os estados inicial e final é igual a:
a) 1/3 b) 2/3 c) 1 d) 4/3 e) 5/3
Resolução:
127 ºC => T1 = 400 K e 327º C => T2 = 600 KEc1/Ec2 = T1/T2 = 400/600 = 2/3
Resposta: b
Exercício 4:
Um mol de um gás perfeito ocupa o volume de 22,4 L, sob pressão de
1 atm e a 0 ºC. Sendo 1 atm = 105 N/m2 e 1 L = 10-3 m3, qual é a energia cinética do gás?
Resolução:
Ec = 3.n.R.T/2 => Ec = 3.p.V/2 = 3.105.22,4.10-3/2 => Ec = 3,36.103 J
Resposta: 3,36.103 J
Exercício 5:
Considere um recipiente contendo um gás perfeito. Analise as afirmações:
I) A energia cinética do gás independe da temperatura a que o gás se encontra.
II) A 0 ºC a energia cinética do gás é nula.
III) A energia cinética média por molécula independe da natureza do gás.
Tem-se:
a) Somente a afirmação I) é correta.
b) Somente a afirmação II) é correta.
c) Somente a afirmação III) é correta.
d) Todas as afirmações são corretas.
e) Somente duas das afirmações são corretas.
Resolução:
I) Incorreta. A energia cinética de um determinado número de mols de um gás é diretamente proporcional à temperatura absoluta.
II) Incorreta. 0º C corresponde a T = 273 K
III) Correta. A energia cinética média por molécula (ec = 3.k.T, onde k é a constante de Boltzmann) independe da natureza do gás: Gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula.
x
Resposta: c
x
Exercício 6:
Dois recipientes, A e B, contém gases de naturezas diferentes. Os gases estão à mesma temperatura. O gás do recipiente A tem massa molar maior do que a do recipiente B. Sejam vA e vB as velocidades médias das moléculas de A e B, respectivamente. Pode-se afirmar que:
a) vA = vB
b) vA > vB
c) vA < vB
d) vA = 2vB
e) vA = vB/2
Resolução:
De v2 = 3.R.T/M, sendo MA > MB, resulta que: vA < vB
Resposta: c
Exercícios de revisão
Revisão/Ex 1:
(ACAFE-SC)
Considerando p a pressão, V o volume e N o número de moléculas de um certo gás ideal, a energia cinética média por molécula desse gás pode ser escrita:
a) Np/2V b) 2pV/3N c) 3pN/2V d) 2pN/3V e) 3pV/2N
Resolução:
A energia cinética de um gás ideal é dada por Ec = 3.p.V/2.
Sendo N o número de moléculas, concluímos que a energia cinética média por molécula é ec = 3.p.V/2N
Resposta: e
Revisão/Ex 2:
(UFRN)
Um gás ideal contido num recipiente sofre uma mudança de temperatura de 300 K para 1.200 K. Qual a razão entre as velocidades médias das moléculas desse gás (v300/v1200)?
Resolução:
De v2 = 3.R.T/M e sendo T1 = 300 K e T2 = 1200 K, vem: (v300/v1200)2 = T1/T2 => (v300/v1200)2 = 300/1200 => v300/v1200 = 1/2
Resposta: 1/4
Revisão/Ex 3:
(UPE)
Em relação à teoria cinética molecular dos gases, é CORRETO afirmar que:
a) a energia cinética média de um conjunto de moléculas de um gás depende, apenas e exclusivamente, das massas das moléculas desse gás.
b) quando quadruplicamos a temperatura absoluta de um conjunto de moléculas de um gás, suas moléculas terão velocidade média quadruplicada.
c) quanto maiores as interações entre as moléculas de um gás, mais rigorosamente ele se comportará como um gás ideal.
d) numa mesma temperatura, independentemente das massas molares de cada gás, as moléculas têm energias cinéticas médias iguais.
e) as colisões entre moléculas de um gás perfeito com as paredes do recipiente que as contém são inelásticas para qualquer tipo de gás ideal.
Resolução:
A energia cinética média por molécula é dada por ec = 3.k.T/2, onde k é a constante de Boltzmann. Observe que gases diferentes à mesma temperatura têm a mesma energia cinética média por molécula. Portanto, a alternativa d é a correta.
Resposta: d
Revisão/Ex 4:
(UNIFEI)
De acordo com a teoria cinética dos gases, a energia cinética média das moléculas que constituem um gás é proporcional à temperatura desse gás. Considere um gás à temperatura ambiente (27 ºC), constituído por moléculas de hidrogênio e de oxigênio. Sabendo que as massas atômicas do hidrogênio e do oxigênio são iguais a 1,0 u.m.a. e 16,0 u.m.a., respectivamente, quais moléculas se movem com maiores velocidades: as moléculas de hidrogênio ou as de oxigênio? Justifique.
Resolução:
De v2 = 3.R.T/M, para o mesmo T e Mhidrogênio < Moxigênio, concluímos que as moléculas de hidrogênio se movem com maiores velocidades.
Revisão/Ex 5:
(UFU-MG)
Considere uma amostra de hidrogênio e outra de oxigênio, ambas a uma mesma temperatura. Sabe-se que a massa molecular do hidrogênio é 3,3.10-27 kg e a do oxigênio é 53.10-27 kg. Podemos afirmar que:
a) Se duplicarmos a temperatura absoluta das amostras , os valores das energias cinéticas médias das moléculas não se alteram.
b) A energia cinética das moléculas de hidrogênio é menor que a energia cinética das moléculas de oxigênio.
c) A velocidade média das moléculas de oxigênio é maior que a velocidade média das moléculas de hidrogênio.
d) A energia cinética das moléculas de hidrogênio não se anula no zero absoluto.
e) A energia cinética das moléculas de oxigênio se anula no zero absoluto.
Resolução:
De ec = 3.k.T/2, concluímos que no zero absoluto a energia cinética média das moléculas de um gás ideal é nula.
Resposta: e
Resposta: e
segunda-feira, 27 de maio de 2013
Cursos do Blog - Mecânica
15ª aula
Cinemática vetorial (III)
Borges e Nicolau
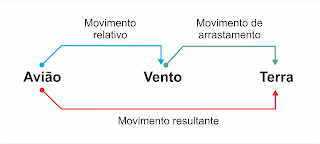
Considere um barquinho movendo-se nas águas de um rio. O movimento do barquinho em relação às águas chama-se movimento relativo.
O movimento das águas que arrastam o barquinho em relação às margens é o movimento de arrastamento.
O movimento do barquinho em relação às margens, isto é, em relação à Terra, é o movimento resultante.
A velocidade do barquinho em relação às águas é a velocidade relativa
(vrel).
A velocidade das águas, isto é, a velocidade da correnteza é a velocidade de arrastamento (varr).
A velocidade do barquinho em relação às margens é a velocidade resultante (vres).
Tem-se a relação vetorial:
Portanto: a velocidade do movimento resultante é a soma vetorial das velocidades dos movimentos relativo e de arrastamento.
Considere os casos:
Exercícios básicos
Exercício 1:
Um barco desce um rio com velocidade em relação às margens de módulo 20 m/s e, a seguir, sobe o rio com velocidade de 8,0 m/s também em relação às margens. Determine o módulo da velocidade do barco em relação às águas, considerado o mesmo na subida e na descida e o módulo da velocidade da correnteza.
Resolução:
Vamos indicar por vres, vrel e varr os módulos das velocidades resultante, relativa e de arrastamento. Podemos escrever:
Barco descendo o rio: vres = vrel + varr => 20 = vrel + varr (1)
Barco subindo o rio: vres = vrel - varr => 8,0 = vrel - varr (2)
De (1) e (2):
vrel = 14 m/s e varr = 6,0 m/s
Respostas: 14 m/s e 6,0 m/s
Exercício 2:
Um ônibus se desloca em movimento retilíneo e uniforme com velocidade de módulo 72 km/h, em relação a uma estrada.
Um menino sai da parte traseira do ônibus e com passadas regulares se desloca até à parte dianteira, percorrendo em 5 s a distância de 10 m em relação ao ônibus. Determine:
a) O módulo da velocidade do menino em relação ao ônibus e em relação à estrada.
b) A distância que o menino percorre, em relação à estrada ao se deslocar da parte traseira até à parte dianteira do ônibus.
Sugestão:
Resolução:
a) vrel = Δsrel/Δt = 10 m/5 s => vrel = 2m/s = 7,2 km/h
vres = vrel + varr => vres = 2 + 20 => vres = 22 m/s = 79,2 km/h
b) vres = Δsrel/Δt => 22 = Δsrel/5 => Δsrel = 110 m
Respostas:
a) 2m/s = 7,2 km/h e 22 m/s = 79,2 km/h;
b) 110 m
Exercício 3:
Um barco atravessa um rio de margens paralelas e de largura 2,0 km, com velocidade em relação à correnteza de módulo 8,0 km/h. O barco sai de um ponto A de uma margem e mantém seu eixo sempre perpendicular à correnteza, atingindo a outra margem.
A velocidade da correnteza é constante e de módulo igual a 6,0 km/h. Determine:
a) o módulo da velocidade resultante do barco;
b) a duração da travessia;
c) o módulo da velocidade resultante do barco para que ele saia de A e atinja um ponto B da margem oposta, exatamente em frente ao ponto A de partida.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (8,0)2 + (6,0)2 => vres = 10 km/h
b) vrel = Δsrel/Δt => 8,0 = 2,0/Δt => Δt = (1/4) h = 15 min
c) (vrel)2 = (vres)2 + (varr)2 => (8,0)2 = (vres)2 + (6,0)2 =>
vres = √28 km/h ≅ 5,3 km/h
Respostas: a) 10 km/h; b) 15 min c) √28 km/h => ≅ 5,3 km/h
Exercício 4:
Um avião possui em relação à Terra uma velocidade de 600 km/h, na direção norte-sul e sentido de sul para norte. Repentinamente o avião enfrenta um forte vento com velocidade, em relação à Terra, de 100 km/h, na direção oeste-leste e no sentido de oeste para leste. Para que o avião continue em sua rota original, qual deve ser o módulo da velocidade do avião em relação ao ar e qual é aproximadamente o ângulo que o eixo longitudinal do avião deve fazer com a direção norte-sul? É dada a tabela:
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (600)2 + (100)2 =>
vrel = √37.102 km/h ≅ 608,3 km/h
tg θ = varr/vrel = 100/608,3 ≅ 0,17 => θ ≅ 10º
Respostas: √37.102 km/h => 608,3 km/h; aproximadamente 10º
Exercício 5:
A chuva cai verticalmente com velocidade de módulo 3,0 m/s, em relação ao solo. Não há ventos. Uma pessoa caminha horizontalmente com velocidade de módulo √3 m/s. Para não se molhar ela inclina seu guarda-chuva de um ângulo θ com a horizontal. Qual é o valor de θ?
Sugestão:
Exercícios de revisão
Revisão/Ex 1:
(U. Mackenzie-SP)
Uma lancha, subindo um rio, percorre em relação às margens, 2,34 km em 1 h 18 min. Ao descer o rio, percorre a mesma distância em 26 min. Observa-se que, tanto na subida como na descida, o módulo da velocidade da lancha em relação á água é o mesmo. O módulo da velocidade da correnteza em relação às margens é:
a) 5,4 km/h b) 4,5 km/h c) 3,6 km/h d) 2,7 km/h e) 1,8 km/h
Resolução:
Barco subindo o rio:
vres = vrel - varr => 2,34km/1,3h = vrel - varr => 1,8 km/h = vrel - varr (1)
Barco descendo o rio:
vres = vrel + varr => 2,34km/(26/60)h = vrel + varr => 5,4 km/h = vrel + varr (2)
De (1) e (2):
vrel = 3,6 km/h e varr = 1,8 km/h (velocidade da correnteza)
Resposta: e
Revisão/Ex 2:
(ITA-SP)
Um barco, com motor em regime constante, desce um trecho retilíneo de um rio em 2,0 h e sobe o mesmo trecho em 4,0 h. Quanto tempo levará o barco para percorrer o mesmo trecho, rio abaixo, com o motor desligado? Admita que a velocidade da correnteza seja constante.
a) 3,0 h b) 4,0 h c) 6,0 h d) 8,0 h e) 10 h
Resolução:
Barco desce o rio: vres = vrel + varr => d/2,0 = vrel + varrr (1)
Barco sobe o rio: vres = vrel - varr => d/4,0 = vrel - varrr (2)
(1) – (2): d/4,0 = 2.varr (3)
Para percorrer o mesmo trecho, rio abaixo, com o motor desligado, a velocidade do barco é a mesma da correnteza, isto é, de arrastamento.
Assim, de (3), vem:
d/4,0 = 2.(d/Δt ) => Δt = 8,0 h
Resposta: d
Revisão/Ex 3:
(UFMT)
Uma pessoa tem velocidade, relativa a uma esteira, de módulo 1,5 m/s e direção perpendicular à da velocidade de arrastamento da esteira. A largura da esteira é de 30 m e sua velocidade de arrastamento, em relação ao solo, tem módulo igual a 2,0 m/s. Calcule:
a) o módulo da velocidade da pessoa em relação ao solo.
b) a distância percorrida pela pessoa, em relação ao solo, ao atravessar a esteira.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (1,5)2 + (2,0)2 => vres = 2,5 m/s
b) vrel = AB/Δt => 1,5 = 30/Δt => Δt = 20 s
vres = AC/Δt => 2,5 = AC/20 => AC = 50 m
Respostas: a) 2,5 m/s b) 50 m
Revisão/Ex 4:
(EFEI-MG)
Um barco atravessa um rio seguindo a menor distância entre as margens que são paralelas. Sabendo que a largura do rio é de 2,0 km, que a travessia é feita em 15 min e que a velocidade da correnteza é 6,0 km/h, podemos afirmar que a velocidade do barco em relação à água é:
a) 2,0 km/h
b) 6,0 km/h
c) 8,0 km/h
d) 10 km/h
e) 14 km/h
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (2,0km/0,25h)2 + (6,0)2 => vrel = 10 km/h
Resposta: d
Revisão/Ex 5:
(Fatec-SP)
Sob chuva que cai verticalmente, uma pessoa caminha horizontalmente com velocidade 1,0 m/s, inclinando o guarda-chuva a 30º (em relação à vertical), para resguardar-se o melhor possível. Dado que tg 60º = 1,7, a velocidade da chuva em relação ao solo:
a) é 1,7 m/s
b) é 2,0 m/s
c) é 0,87 m/s
d) depende do vento.
e) depende da altura da nuvem de origem.
Resolução:
Cinemática vetorial (III)
Borges e Nicolau
Composição de movimentos
Considere um barquinho movendo-se nas águas de um rio. O movimento do barquinho em relação às águas chama-se movimento relativo.
O movimento das águas que arrastam o barquinho em relação às margens é o movimento de arrastamento.
O movimento do barquinho em relação às margens, isto é, em relação à Terra, é o movimento resultante.
A velocidade do barquinho em relação às águas é a velocidade relativa
(vrel).
A velocidade das águas, isto é, a velocidade da correnteza é a velocidade de arrastamento (varr).
A velocidade do barquinho em relação às margens é a velocidade resultante (vres).
Tem-se a relação vetorial:
Portanto: a velocidade do movimento resultante é a soma vetorial das velocidades dos movimentos relativo e de arrastamento.
Considere os casos:
Clique para ampliar
Clique para ampliar
Clique para ampliar
Clique para ampliar
Exercícios básicos
Exercício 1:
Um barco desce um rio com velocidade em relação às margens de módulo 20 m/s e, a seguir, sobe o rio com velocidade de 8,0 m/s também em relação às margens. Determine o módulo da velocidade do barco em relação às águas, considerado o mesmo na subida e na descida e o módulo da velocidade da correnteza.
Resolução:
Vamos indicar por vres, vrel e varr os módulos das velocidades resultante, relativa e de arrastamento. Podemos escrever:
Barco descendo o rio: vres = vrel + varr => 20 = vrel + varr (1)
Barco subindo o rio: vres = vrel - varr => 8,0 = vrel - varr (2)
De (1) e (2):
vrel = 14 m/s e varr = 6,0 m/s
Respostas: 14 m/s e 6,0 m/s
Exercício 2:
Um ônibus se desloca em movimento retilíneo e uniforme com velocidade de módulo 72 km/h, em relação a uma estrada.
Um menino sai da parte traseira do ônibus e com passadas regulares se desloca até à parte dianteira, percorrendo em 5 s a distância de 10 m em relação ao ônibus. Determine:
a) O módulo da velocidade do menino em relação ao ônibus e em relação à estrada.
b) A distância que o menino percorre, em relação à estrada ao se deslocar da parte traseira até à parte dianteira do ônibus.
Sugestão:
Clique para ampliar
Resolução:
a) vrel = Δsrel/Δt = 10 m/5 s => vrel = 2m/s = 7,2 km/h
vres = vrel + varr => vres = 2 + 20 => vres = 22 m/s = 79,2 km/h
b) vres = Δsrel/Δt => 22 = Δsrel/5 => Δsrel = 110 m
Respostas:
a) 2m/s = 7,2 km/h e 22 m/s = 79,2 km/h;
b) 110 m
Exercício 3:
Um barco atravessa um rio de margens paralelas e de largura 2,0 km, com velocidade em relação à correnteza de módulo 8,0 km/h. O barco sai de um ponto A de uma margem e mantém seu eixo sempre perpendicular à correnteza, atingindo a outra margem.
A velocidade da correnteza é constante e de módulo igual a 6,0 km/h. Determine:
a) o módulo da velocidade resultante do barco;
b) a duração da travessia;
c) o módulo da velocidade resultante do barco para que ele saia de A e atinja um ponto B da margem oposta, exatamente em frente ao ponto A de partida.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (8,0)2 + (6,0)2 => vres = 10 km/h
b) vrel = Δsrel/Δt => 8,0 = 2,0/Δt => Δt = (1/4) h = 15 min
c) (vrel)2 = (vres)2 + (varr)2 => (8,0)2 = (vres)2 + (6,0)2 =>
vres = √28 km/h ≅ 5,3 km/h
Respostas: a) 10 km/h; b) 15 min c) √28 km/h => ≅ 5,3 km/h
Exercício 4:
Um avião possui em relação à Terra uma velocidade de 600 km/h, na direção norte-sul e sentido de sul para norte. Repentinamente o avião enfrenta um forte vento com velocidade, em relação à Terra, de 100 km/h, na direção oeste-leste e no sentido de oeste para leste. Para que o avião continue em sua rota original, qual deve ser o módulo da velocidade do avião em relação ao ar e qual é aproximadamente o ângulo que o eixo longitudinal do avião deve fazer com a direção norte-sul? É dada a tabela:
Clique para ampliar
Sugestão:
Clique para ampliar
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (600)2 + (100)2 =>
vrel = √37.102 km/h ≅ 608,3 km/h
tg θ = varr/vrel = 100/608,3 ≅ 0,17 => θ ≅ 10º
Respostas: √37.102 km/h => 608,3 km/h; aproximadamente 10º
Exercício 5:
A chuva cai verticalmente com velocidade de módulo 3,0 m/s, em relação ao solo. Não há ventos. Uma pessoa caminha horizontalmente com velocidade de módulo √3 m/s. Para não se molhar ela inclina seu guarda-chuva de um ângulo θ com a horizontal. Qual é o valor de θ?
Clique para ampliar
Sugestão:
Clique para ampliar
Resolução:
tg θ = vres/varr = 3/√3 = √3 => θ = 60º
Resposta: 60º
Revisão/Ex 1:
(U. Mackenzie-SP)
Uma lancha, subindo um rio, percorre em relação às margens, 2,34 km em 1 h 18 min. Ao descer o rio, percorre a mesma distância em 26 min. Observa-se que, tanto na subida como na descida, o módulo da velocidade da lancha em relação á água é o mesmo. O módulo da velocidade da correnteza em relação às margens é:
a) 5,4 km/h b) 4,5 km/h c) 3,6 km/h d) 2,7 km/h e) 1,8 km/h
Resolução:
Barco subindo o rio:
vres = vrel - varr => 2,34km/1,3h = vrel - varr => 1,8 km/h = vrel - varr (1)
Barco descendo o rio:
vres = vrel + varr => 2,34km/(26/60)h = vrel + varr => 5,4 km/h = vrel + varr (2)
De (1) e (2):
vrel = 3,6 km/h e varr = 1,8 km/h (velocidade da correnteza)
Resposta: e
Revisão/Ex 2:
(ITA-SP)
Um barco, com motor em regime constante, desce um trecho retilíneo de um rio em 2,0 h e sobe o mesmo trecho em 4,0 h. Quanto tempo levará o barco para percorrer o mesmo trecho, rio abaixo, com o motor desligado? Admita que a velocidade da correnteza seja constante.
a) 3,0 h b) 4,0 h c) 6,0 h d) 8,0 h e) 10 h
Resolução:
Barco desce o rio: vres = vrel + varr => d/2,0 = vrel + varrr (1)
Barco sobe o rio: vres = vrel - varr => d/4,0 = vrel - varrr (2)
(1) – (2): d/4,0 = 2.varr (3)
Para percorrer o mesmo trecho, rio abaixo, com o motor desligado, a velocidade do barco é a mesma da correnteza, isto é, de arrastamento.
Assim, de (3), vem:
d/4,0 = 2.(d/Δt ) => Δt = 8,0 h
Resposta: d
Revisão/Ex 3:
(UFMT)
Uma pessoa tem velocidade, relativa a uma esteira, de módulo 1,5 m/s e direção perpendicular à da velocidade de arrastamento da esteira. A largura da esteira é de 30 m e sua velocidade de arrastamento, em relação ao solo, tem módulo igual a 2,0 m/s. Calcule:
a) o módulo da velocidade da pessoa em relação ao solo.
b) a distância percorrida pela pessoa, em relação ao solo, ao atravessar a esteira.
Resolução:
a) (vres)2 = (vrel)2 + (varr)2 => (vres)2 = (1,5)2 + (2,0)2 => vres = 2,5 m/s
b) vrel = AB/Δt => 1,5 = 30/Δt => Δt = 20 s
vres = AC/Δt => 2,5 = AC/20 => AC = 50 m
Respostas: a) 2,5 m/s b) 50 m
Revisão/Ex 4:
(EFEI-MG)
Um barco atravessa um rio seguindo a menor distância entre as margens que são paralelas. Sabendo que a largura do rio é de 2,0 km, que a travessia é feita em 15 min e que a velocidade da correnteza é 6,0 km/h, podemos afirmar que a velocidade do barco em relação à água é:
a) 2,0 km/h
b) 6,0 km/h
c) 8,0 km/h
d) 10 km/h
e) 14 km/h
Resolução:
(vrel)2 = (vres)2 + (varr)2 => (vrel)2 = (2,0km/0,25h)2 + (6,0)2 => vrel = 10 km/h
Resposta: d
Revisão/Ex 5:
(Fatec-SP)
Sob chuva que cai verticalmente, uma pessoa caminha horizontalmente com velocidade 1,0 m/s, inclinando o guarda-chuva a 30º (em relação à vertical), para resguardar-se o melhor possível. Dado que tg 60º = 1,7, a velocidade da chuva em relação ao solo:
a) é 1,7 m/s
b) é 2,0 m/s
c) é 0,87 m/s
d) depende do vento.
e) depende da altura da nuvem de origem.
Resolução:
tg 60° = vres/varr => 1,7 = vres/1,0 => vres = 1,7 m/s
Resposta: a
Resposta: a
Assinar:
Postagens (Atom)