Cursos do Blog - Mecânica

Movimento vertical no vácuo

Borges e Nicolau

x

O movimento vertical no vácuo é um caso particular de movimento uniformemente variado (MUV).

A aceleração α é igual à aceleração da gravidade g. 

Um móvel lançado verticalmente para cima, no vácuo, descreve um movimento uniformemente variado retardado, atingindo a altura máxima quando sua velocidade escalar, cujo módulo decresce com o tempo, torna-se igual a zero.

Ao descer, a velocidade escalar do móvel aumenta em módulo, o movimento é acelerado. A velocidade com que o móvel atinge o solo é, em módulo, igual à velocidade de lançamento. O tempo de subida é igual ao tempo de descida.

Animação:
Movimento vertical no vácuo
Clique aqui

Exercícios Básicos

Exercício 1:
Na superfície terrestre a aceleração da gravidade “g” tem um valor próximo
de 10 m/s². Na prática isso significa que a velocidade de um corpo abandonado em queda livre, aumenta 10 m/s a cada segundo. Ou seja, no primeiro segundo o corpo atinge 10 m/s, depois, em intervalos de um segundo, 20 m/s, 30 m/s, 40 m/s, 50 m/s e assim por diante.
Em 5 segundos de queda, portanto, a velocidade é igual a  
50 m/s = (50 x 3,6) km/h = 180 km/h.
Você sabe que quando a aceleração é constante, o movimento é uniformemente variado. (MUV)
Calcule:
a) a altura da qual um corpo partiu do repouso e atingiu o solo com
velocidade de 50 m/s;
b) o tempo de queda.

Resolução: 

a) Adotando-se a origem no ponto de partida e orientando-se a trajetória para baixo, temos de acordo com a  equação  de Torricelli:
v² = v0² + 2.g.Δs => (50)² = 2.10.H => H = 125 m

b) s = (g.t²)/2 => H = (g.tq²)/2 => tq = √(2.H/g) => tq = √(2.125/10) => tq = 5 s

Respostas:
a) H = 125 m
b) t = 5 s

Exercício 2:
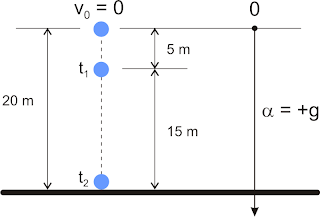
Uma pedra é abandonada de uma altura igual a 20 m. Determine o intervalo de tempo decorrido para a pedra percorrer os últimos 15 m de queda. Considere
g = 10 m/s² e despreze a resistência do ar.

Resolução:

 s = (g.t²)/2 => 5 = (10.t1²)/2 => t1 = 1 s
s = (g.t²)/2 => 20 = (10.t2²)/2 => t2 = 2 s
Δt = t2 - t1 = 2 s - 1 s = 1 s

Resposta: Δt = 1 s

Exercício 3:
Você faz uma pequena bolinha de papel e a lança verticalmente para cima com velocidade de 5 m/s. Quanto tempo a bolinha demora para voltar à sua mão. Qual é a altura máxima atingida pela bolinha. Considere g = 10 m/s² e despreze a resistência do ar.

Resolução: 

 
Vamos calcular o tempo de subida (ts)

v = v0 - g.t => 0 = v0 - g.ts => ts = v0/g => ts = 5/10 => ts = 0,5 s

O tempo de descida é igual ao tempo de subida:

td = ts = 0,5 s

Tempo total:

t = ts + td = 1s

Equação  de Torricelli:

v² = v0² + 2.g.Δs => (5)² = 2.10.H => H = 1,25 m

Resposta: t = 1 s; H = 1,25 m

Exercício 4:
Uma bolinha é abandonada de uma altura H e percorre no último segundo de queda a distância 3H/4. Despreze a resistência do ar e adote g = 10 m/s². Determine o valor de H.

Resolução:

s = (g.t²)/2 => H/4 = [g.(tq-1)²]/2 (1)
s = (g.t²)/2 => H = (g.tq²)/2 (2)
(2) ÷ (1) => 4 = tq²/(tq-1)² => 2 = tq/(tq-1) => tq = 2 s
De (2), vem: H = 20 m

Resposta: H = 20 m

Exercício 5:
De uma altura igual a 40 m lança-se verticalmente para baixo uma bolinha com velocidade 10 m/s. Depois de 1 s, lança-se do mesmo ponto, também verticalmente para baixo, outra bolinha com a mesma velocidade inicial da primeira. Qual é a distância entre elas no instante que a primeira bolinha atinge o solo? Despreze a resistência do ar e considere g = 10 m/s².

Resolução:

Vamos determinar o instante em que a primeira bolinha (A) atinge o solo.

s = s0 + v0.t + (1/2).g.t² => 40 = 0 + 10.t + 5.t² => t = 2 s

Como a bolinha B foi lançada 1 s depois, devemos achar o espaço ocupado por ela no instante 2 s - 1 s = 1 s:

s = s0 + v0.t + (1/2).g.t² => s = 0 + 10.1 + 5.(1)² => s = 15 m.

Assim, a distância entre as bolinhas é de 40 m - 15 m = 25 m

Resposta: d = 25 m

Exercício 6:
Um helicóptero sobe verticalmente em movimento uniforme e com velocidade 10 m/s. Ao atingir a altura de 75 m um pequeno parafuso desprende-se do helicóptero. Quanto tempo o parafuso leva para atingir o solo? Despreze a resistência do ar e adote g = 10 m/s².

Resolução:

Vamos adotar:
Origem dos tempos: instante em que o parafuso se desprende
Origem dos espaços: posição em que o parafuso de desprende
Orientação da trajetória para baixo.
Observe que a velocidade inicial do parafuso é a própria velocidade do helicóptero. Como orientamos a trajetória para baixo, temos v0 = -10 m/s.

s = s0 + v0.t + (1/2).g.t² = 75 = 0 – 10.t +5.t² => t = 5 s

Resposta: t = 5 s