x
Borges e Nicolau
x
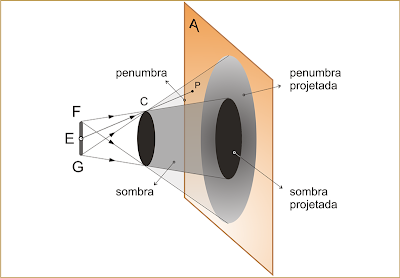
Vamos considerar uma fonte puntiforme F, um disco opaco C e um anteparo A. O disco está disposto paralelamente ao anteparo.
x
Observa-se no anteparo uma sombra projetada de forma semelhante à do corpo opaco C, o que evidencia o fato de a luz se propagar em linha reta. Entre o disco C e o anteparo A, forma-se um tronco de cone que não é iluminado pela fonte F, sendo denominado sombra.
x
Foto: M. Z. Ferraro
Se invés de uma fonte puntiforme F tivéssemos uma fonte extensa FG, como, por exemplo, uma lâmpada fluorescente, notaríamos que além da sombra e da sombra projetada teríamos regiões parcialmente iluminadas denominadas penumbra e penumbra projetada. Observe que o ponto P da penumbra é iluminado apenas pelo trecho FE da fonte extensa.
x
Eclipses do Sol
x
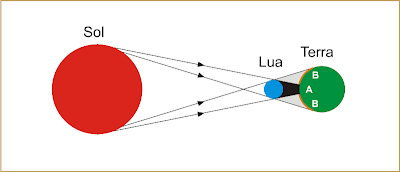
Considerando o Sol como fonte de luz e a Lua como corpo opaco, ocorre eclipse do Sol quando a sombra e a penumbra da Lua interceptam a Terra (anteparo). O eclipse do Sol é total para os habitantes da Terra que se encontram na sombra projetada (A) e parcial para aqueles que se encontram na penumbra projetada (B).
x
x
Eclipses da Lua
x
Considerando o Sol como fonte de luz e a Terra como corpo opaco, ocorre eclipse total da Lua quando ela inteira está imersa na sombra da Terra. O eclipse é parcial quando parte da Lua está imersa na sombra da Terra.
x
As órbitas da Lua em torno da Terra, e da Terra, em torno do Sol, não pertencem ao mesmo plano. Em determinadas ocasiões, pode acontecer de os três astros se alinharem justamente no ponto em que a órbita da Lua intercepta o plano da órbita da Terra, ocorrendo o eclipse.
x
Câmara escura de orifício
x
A câmara escura de orifício é uma caixa de paredes opacas existindo em uma delas um pequeno orifício, por onde pode penetrar luz.
x
Um objeto AB é colocado diante da parede que possui o orifício. Os raios de luz, que partem do objeto e passam pelo orifício determinam, na parede oposta à do orifício, uma figura A’B’, semelhante ao objeto, mas invertida.
x
Essa figura é chamada imagem A’B’ do objeto AB. A imagem é semelhante ao objeto e invertida. Isto evidencia o fato de a luz se propagar em linha reta.
x
x
Sejam (o) e (i) as alturas do objeto e da imagem e p e p' suas distâncias à parede que contém o orifício, respectivamente. Da semelhança entre os triângulos A’B’O e ABO, obtemos:
x
i/o = p'/p
x
Para que um observador externo veja a imagem, a parede onde ela se forma deve ser substituída por uma folha de papel vegetal. A imagem vista pelo observador, além de invertida, troca o lado direito pelo lado esquerdo e vice-versa.
x
Exercícios Básicos
x
Exercício 1:Entre uma fonte puntiforme e uma parede, coloca-se um lápis de 20 cm de altura. A fonte de luz e o centro do lápis estão numa mesma reta perpendicular à parede. O lápis se encontra a 20 cm da fonte e a 60 cm da parede. Determine o comprimento da sombra do lápis projetada na parede.
x
Resolução:Da semelhança dos triângulos FAB e FCD, vem:
L/20 = 80/20 => L = 80 cm
Resposta: 80 cm
Exercício 2:
Analise as afirmações e assinale as corretas:
x
I) A formação de penumbra de um corpo opaco ocorre quando a fonte de luz é extensa. II) O eclipse do Sol só ocorre numa fase de Lua Cheia e, portanto, todos os meses têm-se eclipses do Sol.
III) Quando ocorre eclipse do Sol a posição relativa dos três astros é Sol, Terra e Lua.
IV) Uma pessoa na Terra se situa na penumbra da Lua determinada pelo Sol. Esta pessoa presencia um eclipse parcial do Sol.
x
Resolução:I) Correta. Quando uma fonte de luz extensa é colocada próxima de um corpo opaco observam-se regiões parcialmente iluminadas. São as penumbras.
II) Incorreta. No eclipse do Sol, a posição relativa dos astros é Sol, Lua e Terra. Portanto, o eclipse do Sol ocorre na fase de Lua Nova. Os eclipses não ocorrem todos os meses pois as órbitas da Lua em torno da Terra e da Terra em torno do Sol não pertencem ao mesmo plano. Os eclipses ocorrem quando a orbita da Lua intercepta o plano da órbita da Terra e ainda deve haver um alinhamento entre os três astros.
III) Incorreta. A posição relativa dos astros é Sol, Lua e Terra.
IV) Correta. Estando na penumbra da Lua determinada pelo Sol o eclipse é parcial.
Respostas: I) e IV)
Exercício 3:
a) Esquematize a posição relativa dos três astros Sol, Terra e Lua, durante um eclipse total da Lua.
b) Em qual fase da Lua ocorre o eclipse lunar?
x
Resolução:
a) A posição relativa dos três astros é Sol, Terra e Lua:
b) Se não estivesse ocorrendo eclipse a Lua voltaria seu hemisfério iluminado para a Terra. Portanto, a fase é de Lua Cheia.
Respostas:
a) Sol; Terra; Lua
b) Lua Cheia
Exercício 4:
Um objeto AB de altura 10 cm encontra-se a 30 cm de uma câmara escura de orifício, cujo comprimento é de 45 cm.
a) Qual é a altura da imagem?
b) Aproxima-se o objeto da câmara. A altura da imagem aumenta ou diminui?
x
Resolução:
a) o = 10 cm; p = 30 cm e p' = 45 cm
De i/o = p'/p, vem: i/10 = 45/30 => i = 15 cmb) Aproximando-se o objeto da câmara o valor de p diminui e portanto a altura i da imagem aumenta.
Respostas:
a) 15 cm; b) Aumenta
Exercício 5:
Uma placa na qual está escrita a letra P é iluminada e disposta em frente a uma câmara escura de orifício. A parede onde se forma a imagem é de vidro fosco.
Esquematize a imagem que se forma nesta parede e que é vista pelo observador O.
x
Resolução:
A imagem vista pelo observador é invertida e troca a direita pela esquerda e vice-versa. Assim, temos: