Questões de 01 a 10
Borges e Nicolau
1. (UFAC)
A temperatura em Rio Branco, em certo dia, sofreu uma variação de
15 ºC. Na escala Fahrenheit, essa variação corresponde a:
A) 108 ºF
B) 71 ºF
C) 44 ºF
D) 27 ºF
E) 1 ºF
Resolução:
ΔθC/5 = ΔθF/9 => 15/5 = ΔθF/9 => ΔθF = 27 ºF
Uma variação de 15 ºC corresponde a uma variação de 27 ºF
Alternativa: D
2. (UFPI)
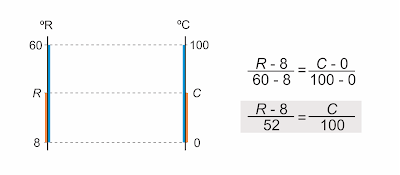
Em 1708, o físico dinamarquês Olé Römer, propôs uma escala termométrica a álcool, estabelecendo 60 graus para água em ebulição e zero graus para uma mistura de água com sal, resultando em 8 graus a temperatura da fusão do gelo. Além da possível utilização científica, essa escala teria a vantagem de nunca marcar temperaturas negativas em Copenhague, o que era desejo dos fabricantes da época, devido a superstições. A temperatura média normal do corpo humano na escala de Römer e a menor temperatura, em graus Celsius, que Copenhague poderia registrar nos termômetros de escala Römer, são nessa seqüência dadas, aproximadamente, por:
Dado: considere a temperatura normal do corpo humano igual a 36,5 ºC.
A) 27,0 ºC e 8,0 ºR
B) -15,4 ºR e 36,5 ºC
C) 27,0 ºR e -15,4 ºC
D) 27,0 ºC e 0,0 ºR
E) 36,5 ºR e -15,4 ºC
Resolução:
Relacionando as escalas Römer e Celsius:
Temperatura normal do corpo humano (36,5 ºC) em ºR:
(R-8)/52 = 36,5/100 => R-8 = 18,98 => R = 26,98 => R ≈ 27 ºR
Temperatura mínima em Copenhague (0 ºR) em ºC
(0-8)/52 = C/100 => C = -15,3846 => C ≈ -15,4 ºC
Alternativa: C
3. (UFPI)
O Aquecimento Global é um fenômeno climático de larga extensão. As previsões mais catastróficas para a região Amazônica incluem o desaparecimento completo da floresta se a temperatura média da região tiver um aumento superior aos 5 ºC. Com isso a temperatura média anual da cidade de Manaus passaria a ser de 33 ºC, que lida na escala Kelvin corresponderia a:
A) 300 K
B) 310 K
C) 290 K
D) 306 K
E) 302 K
Resolução:
T = θC + 273 => T = 33 + 273 => T = 306 K
Alternativa: D
4. (UFAC)
Uma barra de alumínio tem 100 cm, a 0 ºC. Qual o acréscimo de comprimento dessa barra quando sua temperatura chega a 100 ºC.
(Dado: αAl = 2,4 x 10-5 ºC-1).
A) 0,12 cm
B) 0,24 cm
C) 0,36 cm
D) 0,48 cm
E) 0,60 cm
Resolução:
ΔL = L0.α.Δθ => ΔL = 100.2,4.10-5.100 => ΔL = 0,24 cm
Alternativa: B
5. (UFV-MG)
Duas barras, 1 e 2, possuem coeficientes de dilatação linear α1 e α2, respectivamente, sendo α1 > α2. A uma certa temperatura To os comprimentos das duas barras são iguais a Lo. O gráfico que melhor representa o comprimento das barras em função da temperatura é:
Clique para ampliar
Resolução:
Sabendo-se que ΔL = L0.α.Δθ, a barra de maior coeficiente de dilataçâo (α1 > α2) terá maior variação de comprimento (ΔL) para variações de temperaturas iguais.
Alternativa: A
6. (UEMS)
Na temperatura ambiente, dois cubos A e B possuem arestas iguais a L e coeficientes de dilatação volumétricas γA e γB, respectivamente, com
γA = (3/2)γB. Supondo que os dois cubos sofram a mesma variação de volume, pode-se afirmar que a relação entre as variações de temperatura dos cubos A e B é:
A) ΔθA = (1/4)ΔθB
B) ΔθA = (1/3)ΔθB
C) ΔθA = (1/2)ΔθB
D) ΔθA = (2/3)ΔθB
E) ΔθA = ΔθB
Resolução:
ΔVA = V0A.γA.ΔθA => ΔVB = V0B.γB.ΔθB => γA = 3/2γB
ΔVA = ΔVB => L3.γA.ΔθA = L3.γB.ΔθB
ΔθA/ΔθB = γB/γA
ΔθA/ΔθB = 2/3 => ΔθA = (2/3)ΔθB
Alternativa: D
7. (UECE)
Considerando que os coeficientes de dilatação do aço, do alumínio e do latão são, respectivamente, 11x10-6 ºC-1, 23 x 10-6 ºC-1 e 19 x 10-6 ºC-1, o coeficiente de dilatação linear de uma haste de 10 m, constituída por uma barra de aço de 3 m, uma barra de alumínio de 5 m e por uma barra de latão de 2 m, é:
A) 5,3 x 10-6 ºC-1
B) 18,6 x 10-6 ºC-1
C) 23,0 x 10-6 ºC-1
D) 87,0 x 10-6 ºC-1
Resolução:
ΔLbarra = 10.αbarra.Δθ (1)
ΔLbarra = ΔLaço + ΔLalumínio +ΔLlatão
ΔLbarra = 3.11.10-6.Δθ + 5.23.10-6.Δθ + 2.19.10-6.Δθ (2)
Igualando-se (1) e (2), vem:
10.αbarra.Δθ = 3.11.10-6.Δθ + 5.23.10-6.Δθ + 2.19.10-6.Δθ
10.αbarra = (3.11 + 5.23 + 2.19).10-6
αbarra = 18,6.10-6 ºC-1
Alternativa: B
8. (AFA-SP)
Um recipiente tem capacidade de 3.000 cm3 a 20 ºC e está completamente cheio de um determinado líquido. Ao aquecer o conjunto até 120 ºC, transbordam 27 cm3. O coeficiente de dilatação aparente desse líquido, em relação ao material de que é feito o recipiente é, em ºC-1, igual a:
A) 3,0.10-5
B) 9,0.10-5
C) 2,7.10-4
D) 8,1.10-4
Resolução:
ΔVaparente = V0.γaparente.Δθ
27 = 3000.γaparente.100
γaparente = 9,0.10-5 ºC-1
Alternativa: B
9. (UFAM)
O gráfico representa a temperatura dois corpos sólidos A e B de massas iguais, em função da quantidade de calor Q recebida.
Colocando A a 20 ºC em contato com B a 100 ºC e admitindo que a troca de calor só ocorra entre eles, a temperatura final de equilíbrio é em ºC:
A) 50
B) 80
C) 60
D) 70
E) 90
Resolução:
Do gráfico:
Corpo A => Q = 400 cal; ΔθA = 30 ºC => 400 = m.cA.30 (1)
Corpo B => Q = 400 cal; ΔθB = 10 ºC => 400 = m.cB.10 (2)
Igualando-se (1) e (2), vem:
m.cA.30 = m.cB.10 => cB = 3.cA (3)
Na troca de calor entre A e B:
QA + QB = 0
m.cA.(θf-20) + m.cB.(θf-100) = 0 (4)
Substituindo-se (3) em (4), vem:
m.cA.(θf-20) + m.3cA(θf-100) = 0
θf - 20 + 3θf - 300 = 0
4.θf = 320 => θf = 80 ºC
Alternativa: B
10. (FEI-SP)
Um trocador de calor usado na indústria recebe água quente à temperatura de 90 ºC. Deseja-se resfriar esta água até que sua temperatura atinja 50 ºC. Sabendo-se que para isto será utilizada água fria à temperatura de 20 ºC e que não existe perda de calor para o ambiente, qual será a razão entre a massa de água quente e a massa de água fria que deverá ser utilizada?
A) 1,50
B) 0,50
C) 0,75
D) 1,00
E) 1,33
Resolução:
Misturando-se uma certa massa de água (mA) a 90 ºC com outra massa de água (mB) a 20 ºC até atingir a temperatura de equilíbrio de 50 ºC, podemos escrever:
QA + QB = 0
mA.c.(50-90) + mB.c.(50-20) = 0
-40.mA.c + 30.mB.c = 0
40.mA = 30.mB => mA/mB = 3/4 => mA/mB = 0,75
Alternativa: C



Nenhum comentário:
Postar um comentário