Cursos do Blog - Eletricidade

Lei de Pouillet. Associação de geradores.
x
Borges e Nicolau
x
Considere o circuito constituído de um gerador ligado aos terminais de um resistor. Este circuito é percorrido por uma corrente somente e é denominado circuito simples.

A tensão elétrica entre os polos do  gerador (U = E – r.i) é igual à tensão elétrica no resistor (U = R.i). Portanto, podemos escrever:

E - r.i = R.i

E = (r + R).i

i = E/(r + R)

Esta fórmula que permite calcular a intensidade da corrente elétrica num circuito simples recebe o nome de Lei de Pouillet, em homenagem ao físico francês Claude Pouillet.
Se o gerador estiver ligado a uma associação de resistores, determina-se a resistência equivalente R_eq e, a seguir, aplica-se a Lei de Pouillet:

i = E/(r+R_eq)

x
Se tivermos uma associação de geradores, determinamos a fem equivalente e, a seguir, aplicamos a lei de Pouillet. Exemplos:

1º)

i = 3E/(3r+R)

2º)
x

 i = E/[(r/3)+R]

x
Exercícios básicos

Exercício 1:
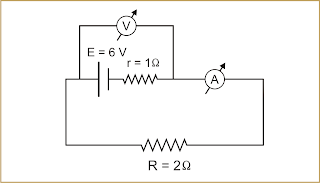
Considere o circuito abaixo. Determine as leituras do amperímetro e do voltímetro, considerados ideais.

Resolução:

Lei de Pouillet:
i = E/(r+R) => i = 6/(1+2) => i = 2 A (leitura do amperímetro)
Leitura do Voltímetro:
U = E – r.i => U = 6 – 1.2 => U = 4 V

Respostas: 2 A; 4 V

Exercício 2:
Determine a intensidade da corrente que atravessa o circuito simples esquematizado abaixo. Ao lado do circuito são representadas as curvas características do gerador e do resistor.

Resolução:

Da curva característica do gerador, tiramos: E = 12 V e I_CC = 6 A.
Sendo I_CC = E/r vem: 6 = 12/r => r = 2 Ω
Da curva característica do resistor: U = R.i => 6 = R.2 => R = 3 Ω
Lei de Pouillet:
i = E/(r+R) => i = 12/(2+3) => i = 2,4 A

Resposta: 2,4 A

Exercício 3:
Para o circuito esquematizado, determine as intensidades das correntes i, i₁ e i₂.

Resolução:

Inicialmente devemos calcular a R_eq: os resistores de 2 Ω e 4 Ω estão ligados em série, sendo 6 Ω a resistência desta associação. Os resistores de 6 Ω e 3 Ω estão em paralelo. A resistência equivalente da associação toda é R_eq = 2 Ω
Lei de Pouillet:
i = E/(r+R_eq) => i = 12/(2+2) => i = 3 A
A ddp no resistor equivalente de 2 Ω é a mesma ddp nos resistores de 3 Ω e de 6 Ω (2 Ω + 4 Ω): U = 2.3 => U = 6 V.
Cálculo de i₁: U = R₁.i₁ => 6 = 6.i₁ => i₁ = 1 A
Cálculo de i₂: U = R₂.i₂ => 6 = 3.i₂ => i₂ = 2 A

Respostas: 3 A; 1 A; 2 A

Exercício 4: 
Determine a leitura do amperímetro ideal inserido no circuito, conforme indicado a seguir. 

Resolução:

i = 3E/(3r+R) => i = 18/(3+9) => i = 1,5 A

Resposta: 1,5 A

Exercício 5: 
Determine a leitura do amperímetro ideal inserido no circuito abaixo.

  
Resolução:

i = E/[(r/3)+R] => i = 6/[(1/3)+3] => i = 1,8 A

Resposta: 1,8 A