Anéis em queda
(IJSO)
Monta-se num plano vertical dois arames, PQ e PS (vertical), de modo que P, Q e S pertençam a uma circunferência de raio R. Dois pequenos anéis, A e B, que passam pelos arames, são abandonados no mesmo instante do ponto P. Despreze os atritos. Sejam tPQ e tPS os intervalos de tempo que os anéis A e B despendem para se deslocarem até Q e S, respectivamente, a partir de P. Seja g a aceleração da gravidade.
Pode-se afirmar que:
a) tPQ = tPS = 2.√(R/g)
b) tPQ = tPS = 2.√(R.g)
c) tPQ = tPS = √(2.R/g)
d) tPQ = tPS.cos θ = 2.√(R/g)
e) tPQ = tPS.cos θ = √(2.R/g)
Resolução:
Anel A
PQ = 1/2.aA.t2 => 2.R.cos θ = 1/2.g.cos θ.(tPQ)2 => tPQ = 2.√(R/g)
Anel B
PS = 1/2.aB.t2 => 2.R = 1/2.g.(tPS)2 => tPS = 2.√(R/g)
Portanto:
tPQ = tPS = 2.√(R/g)
Resposta: a
Relógio em tempo frio
(ITA-SP)
Um relógio de pêndulo simples é montado no pátio de um laboratório em Novosibirsk na Sibéria, utilizando um fio de suspensão de coeficiente de dilatação 1.10-5 °C-1. O pêndulo é calibrado para marcar a hora certa em um bonito dia de verão de 20°C. Em um dos menos agradáveis dias do inverno, com a temperatura a -40°C, o relógio:
a) adianta 52 s por dia.
b) adianta 26 s por dia.
c) atrasa 3 s por dia.
d) atrasa 26 s por dia.
e) atrasa 52 s por dia.
Resolução:
Seja T0 o período do pêndulo a 20°C e T seu período a -40°C
De T0 = 2.π√(L0/g) (1) e T = 2.π√(L/g) (2), vem:
T/T0 = √(L/L0) = √(1+α.Δθ).T0 => T = {√[1+1.10-5.(-40-20)]}.T0
T = (√1-0,0006).T0 => T = (√0,9994).T0 => T = 0,9997.T0
Para T0 = 1 s, vem: T = 0,9997 s (o período diminui e o relógio adianta).
Portanto, para cada segundo o pêndulo adianta 0,0003 s. Em um dia, isto é, em 86400 s o relógio adianta: 0,003 x 86400 s = 26 s
Resposta: b
O maneirismo foi uma movimento artístico que surgiu e se desenvolveu em Roma entre 1520 e 1610, contrapondo-se ao modelo vigente da antiguidade clássica. Uma característica marcante do movimento é a atenção aos detalhes. O artista que apresentamos hoje é o pintor e gravador Girolamo Francesco Maria Mazzola (Parmigianino), considerado o pai da água-forte italiana.
Retrato de uma mulher jovem, possivelmente a condessa Gozzadini
Parmigianino
Notável pintor e gravador italiano do século XVI, Francesco Mazzola nasceu em 1503, em Parma – daí ser conhecido por Parmigianino ou Parmigiano, vindo a falecer em 1540, em Casalmaggiore. Apesar de se conhecer pouco da sua educação, sabe-se que sofreu influências de Correggio e Rafael, como o demonstram as suas pinturas dos primeiros anos (afrescos na Igreja de S. João Evangelista de Parma).
A partir de 1527, afirmou o seu estilo pessoal com obras como a Madonna de S. Petronio de Gamba, a Sagrada Família (Louvre), Sta. Catarina (Museu do Capitólio), Virgem (Palácio de Pitti) e Madonna dal Collo Lungo, que é uma das obras-primas do Maneirismo.
A obra e personalidade de Parmigianino se afirmam em contato com o primeiro maneirismo toscano e através das obras dos grandes mestres Rafael e Michelangelo, conseguindo traduzir de forma original os modelos do Renascimento com uma orientação já plenamente maneiristas. Para ele, a função da arte era transmitir sensações estranhas e excitantes, para o que teria de criar um necessário artificialismo.
Nas crenças da Roma sob Clemente VII, a arte se apresentava indiferente aos valores tradicionais da devoção cristã, os símbolos religiosos e o dogma só possuíam dimensão estética. Com essa visão trabalhou Parmigianino. Nas obras posteriores à sua estadia romana manterá o ar elegante e em certos momentos majestoso, tendo cada vez mais uma beleza abstrata e uma graça artificial.
Retrado de Pier Maria Rossi de Sansecondo
Clique aqui para saber mais.
Cordas vibrantes
(UFPE)
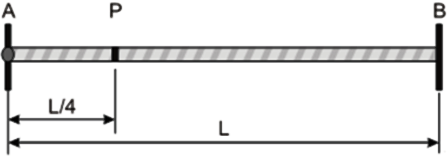
A figura mostra uma corda AB, de comprimento L, de um instrumento musical com ambas as extremidades fixas. Mantendo-se a corda presa no ponto P, a uma distância L/4 da extremidade A, a frequência fundamental da onda transversal produzida no trecho AP é igual a 294 Hz. Para obter um som mais grave o instrumentista golpeia a corda no trecho maior PB. Qual é a frequência fundamental da onda neste caso, em Hz?
Resolução:
As frequências fundamentais no trecho de comprimento L/4 e no trecho de comprimento 3L/4, são, respectivamente, dadas por:
f = v/2.(L/4) e f' = v/2.(3L/4) = (1/3).v/2.(L/4) = (1/3).f =>
f' = (1/3).294 => f' = 98 Hz
Resposta: 98 Hz
O maneirismo foi uma movimento artístico que surgiu e se desenvolveu em Roma entre 1520 e 1610, contrapondo-se ao modelo vigente da antiguidade clássica. Uma característica marcante do movimento é a atenção aos detalhes. O artista que apresentamos hoje é o escultor Giambologna, que podemos dizer, está para o maneirismo como Michelangelo está para o renascimento. Nas semanas seguintes mostraremos outros artistas maneiristas e a influência do movimento nas artes contemporâneas.
Hércules batendo o centauro Nessus, 1599
Giambologna
O escultor flamengo-italiano Giovanni da Bologna (1529-1608) foi, depois de Michelangelo, o escultor mais importante e original do século 16. Um dos expoentes supremos do estilo maneirista, Giovanni foi uma influência importante no desenvolvimento do barroco. Giovanni da Bologna, também conhecido como Giambologna e Jean de Boulogne, nasceu em Douai, Flandres. O primeiro contato de Giambologna com a arte da escultura deu-se no estúdio do escultor flamengo Jacques Dubroeucq.
O rapto das Sabinas - 1582
Em 1554 Giovanni viajou para a Itália e passou dois anos estudando em Roma. Durante uma breve estada em Florença o colecionador e apreciador de arte, Bernardo Vecchietti, reconheceu seu talento e ofereceu-se para apoiá-lo. Dois anos depois Giovanni recebeu sua primeira encomenda dos Médici.
Fonte de Netuno, Praça Maggiore, Bolonha
O notável virtuosismo técnico de Giambologna é particularmente evidente em seus pequenos bronzes. Projetada para ser apreciada pelos conhecedores, a estatueta "Vênus saindo do banho" foi brilhantemente concebida para formar uma quase incrível variedade de pontos de vista sutilmente inter-relacionados. A extrema atenuação e o delicado equilíbrio de outra obra notável, "Mercúrio" (várias versões produzidas entre 1564 e 1580) teria sido impossível em qualquer outro meio.
O Rapto das Sabinas (1582), na Loggia dei Lanzi, Florença, é mais uma das obras-primas de Giovanni cuja gênese é bem documentada pela sobrevivência dos modelos de cera e, neste caso, duas pequenas versões em bronze.
Giambologna permaneceu em Florença a serviço dos Médici até sua morte, em 13 de agosto de 1608.
Vênus saindo do banho, 1572-1573
Clique aqui para saber mais.
O instantâneo abaixo é do dia 4 de agosto de 1945. O marinheiro Carl Muscarello e a enfermeira Edith Shain, em plena Times Square, centro de Nova York, comemoram o final da guerra com um beijo. Alfred Eisenstaedt estava lá e registrou. A foto acabou virando capa da revista Life. O casal nunca mais se encontrou, mas o beijo daquele dia eufórico tornou-se uma das imagens mais marcantes do século XX.
Alfred Eisenstaedt
Alfred Eisenstaedt (Dirschau, 6 de Dezembro de 1898 - Nova Iorque, 24 de Agosto de 1995) foi um fotógrafo e fotojornalista norte-americano nascido na antiga Prússia. A família mudou-se para Berlim, na Alemanha, quando ele tinha oito anos e lá ficou até ao momento em que Adolf Hitler chegou ao poder.
Aos catorze anos um tio ofereceu-lhe uma câmara fotográfica, uma Eastman Kodak nº 3 (uma câmara de fole). Três anos mais tarde foi recrutado para o exército alemão. Em 1918, durante a Primeira Guerra Mundial, a explosão de uma granada afetou-lhe ambas as pernas. Foi o único sobrevivente do ataque e foi mandado ferido para casa. Levou cerca de um ano até poder caminhar de novo sem ajuda, e foi durante a recuperação que se interessou novamente pela fotografia.
Em 1922, tornou-se vendedor de cintos e botões e, com o dinheiro que conseguiu poupar, adquiriu equipamento fotográfico. Ao vender uma foto teve a ideia da possibilidade de viver da fotografia e assim, aos 31 anos, abandonou a profissão de vendedor e passou a fotografar em tempo integral. Dois anos depois da subida de Hitler ao poder emigrou para os Estados Unidos. Em Nova York foi convidado a fazer parte de um novo projeto: a revista Life. Em 1942 naturalizou-se norte-americano e viajou por vários países para documentar os efeitos da guerra: no Japão registou os efeitos da bomba atômica, na Coreia a presença das tropas americanas e na Itália o estado miserável dos pobres.
Funeral de Evita Perón - Buenos-Aires
Durante a sua carreira fotografou personalidades famosas, como Marlene Dietrich, Marilyn Monroe, Ernest Hemingway, JFK e Sophia Loren. Eisenstaedt recebeu inúmeros prêmios. A cidade de Nova York nomeou um dia em sua honra, o presidente George Bush entregou-lhe a Medalha Presidencial das Artes, o ICP (Internacional Center of Photography) atribuiu-lhe o prêmio Masters of Photography, entre outros. Nos seus últimos tempos de vida continuou a trabalhar, supervisionando a impressão das suas fotografias para futuras exposições ou livros.
Clique aqui para saber mais.
Potência e rendimento
(FGV-SP)
A montadora de determinado veículo produzido no Brasil apregoa que a potência do motor que equipa o carro é de 100 HP (1 HP = 750 W). Em uma pista horizontal e retilínea de provas, esse veículo, partindo do repouso, atingiu a velocidade de 144 km/h em 20 s. Sabendo que a massa do carro é de 1 000 kg, o rendimento desse motor, nessas condições expostas, é próximo de:
a) 30%. b) 38%. c) 45%. d) 48%. e) 53%.
Resolução:
A potência total do motor é Pot(total) = 100 HP = 75000 W
Vamos calcular a potência útil:
Pot(util) = τ/Δt => Pot(util = (m.v2/2)/Δt =>
Pot(util) = 1000.(40)2/2)/20 =>
Pot(util) = 40000 W
O rendimento do motor é a razão entre as potências útil e total:
η = Pot(util)/Pot(total) => η = 40000/75000 => η ≅
0,53 = 53%
Resposta: e
